Enunciado
Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.4 - Ex. 80
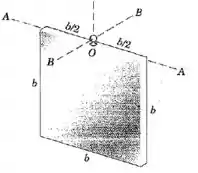
A placa quadrada fina está suspensa por uma cavidade (não mostrada) que se encaixa na pequena esfera de fixação em . Se a placa é levada a oscilar em torno do eixo -, determine o período para pequenas oscilações. Despreze o pequeno deslocamento, massa, e atrito da esfera.
Passo 1
Vamos começar montando uma equação de momentos em relação ao eixo -:
A única força que gera momento em relação a esse eixo é o peso, que age no centro de massa da placa, a uma distância do eixo.
Lembre sempre do sinal negativo, pois o momento favorece o retorno ao ponto de equilíbrio, onde .
Passo 2
Agora vamos olhar para o outro lado da equação, o momento de inércia pode ser calculado com o teorema dos eixos paralelos:
Agora vamos substituir tudo na equação principal:
Para pequenas oscilações podemos aproximar :
E o termo que multiplica é o quadrado da frequência natural de oscilação, então:
Então o período é:
Resposta
O período de pequenas oscilações é .