Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 3.Problemas - Ex. 126
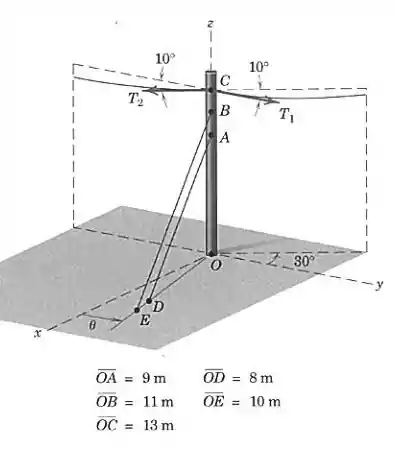
O poste vertical, linha de transmissão e os dois cabos de amarração do Prob. 3/96 são mostrados aqui novamente. Como parte de um estudo do projeto, as seguintes condições são consideradas. A força trativa vale 1000 N e é constante, com ângulo fixo de 10°. O ângulo de 10° para também é fixo, mas o módulo de pode variar desde 0 até 2000 N. Para cada valor de , determine e plote o módulo das tensões idênticas nos cabos e e o ângulo para o qual o momento em será zero. Explicite os valores de e para .
Passo 1
Vamos calcular as componentes de todas as forças nas direções , e , para depois aplicar as equações de equilíbrio. Definindo o valor de , temos as incógnitas e . Como temos 2 incógnitas, conseguimos resolver (pois temos 2 equações de momento em torno de , para a direção e para a direção ).
Passo 2
Primeiro para , temos:
Passo 3
Para :
Passo 4
Agora para e , precisamos determinar a direção das forças em função de calculando os vetores unitários. Primeiro para , temos:
Então temos o vetor unitário na direção :
Passo 5
Faremos o mesmo para :
Passo 6
Agora que temos as forças, vamos fazer os momentos em torno de :
Para a direção :
Mas sabemos que , então:
Finalmente chegamos então ao valor de :
E agora achamos :
Passo 7
Para N, calculamos e :