Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 133

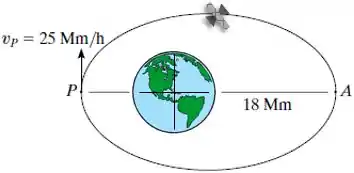
O satélite está em uma órbita elíptica. Quando ele está no perigeu P , sua velocidade é v P = 25   M m / h , e quando ele chega ao ponto A , sua velocidade é v A = 15   M m / h e sua altitude acima da superfície da Terra é 18 Mm. Determine o período do satélite.

Passo 1

O enunciado nos dá as seguintes informações:

Velocidade do satélite no ponto P : v P = 25   M m / h ;

Velocidade do satélite no ponto A : v P = 15   M m / h .

Devemos determinar o período do satélite.

Lembre-se se utilizar as unidades do SI!

A velocidade em metros por segundo no ponto P   é igual a

v P = 25 10 6 m h 1     h 3600     s = 6944,44   m / s

A velocidade em metros por segundo no ponto A   é igual a

v A = 15 10 6 m h 1     h 3600     s = 4166,67   m / s

A Altitude acima da superfície da Terra no ponto A é igual a 18 10 6 m.

Suponha que o raio da Terra é 6378 km;

A massa da Terra é de M e = 5,976(1024) kg;

A massa do Sol é de M s = 1 ,99(1030) kg;

A constante gravitacional é de G = 66,73 10 - 12   m 3 / ( k g   s 2 ) .

Raio da Terra: r T = 6378   k m

Passo 2

Primeiramente, vamos obter os danos no Ponto A .

Analisando a Figura, vemos que

r A = a l t i t u d e + r T = 18 10 6 + 6378 10 3

r A = 24,378 10 6   m

Passo 3

Em seguida, vamos obter os dados do ponto P .

A Equação 13.20 nos informa que

h = r v

onde h é uma constante. Logo,

h = r A v A = 24,378 10 6 4166,67 = 101,575 10 9   m 2 / s  

Como h   é uma constante, temos que

h = r A v A = r P v P

logo,

r P = r A v A v P = 101,575 10 9 6944,44

r P = 14,63 10 6   m

Passo 4

Utilizando os resultados de h ,   r P e r A , podemos encontrar o período T .

Sabemos que

T = π h r p + r a r p r a

Logo,

T = π 101,575 10 9   14,63 10 6 + 24,378 10 6 14,63 10 6 24,378 10 6

T = 430158,48   s

T = 119   h

Resposta

T = 119   h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O cursor A de 3k g se encaixa com folga na ranhura lisa de 45 ° no disco, que gira em um plano horizontal em torno do seu centro O . Se A é mantido em posição por um cordão fixo no ponto B , determine
Uma pequena conta de massa m é conduzida por um aro circular de raio r que gira em torno de um eixo vertical fixo. Mostre como se pode determinar a velocidade angular ω do aro pela observação do ângul
O braço robótico está se elevando e prolongando simultaneamente. Em um determinado instante, θ = 30 ° , θ ˙ = 40g r a u s / s , θ ¨ = 120g r a u s / s ² ², l = 0,5m , l ˙ = 0,4m / s e l ¨ = - 0,3m / s
O pequeno objeto de massa m é colocado sobre a superfície cônica giratória no raio mostrado. Se o coeficiente de atrito estático entre o objeto e a superfície rotativa é 0,8 , calcule a máxima velocid
O pequeno objeto é colocado sobre a superfície interna do prato cônico no raio mostrado. Se o coeficiente de atrito estático entre o objeto e a superfície cônica é 0,30 , para qual faixa de velocidade