Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 82
A viga uniforme de 50 kg (barra fina) está estendida no solo quando o homem exerce uma força F = 300 N na corda, a qual passa sobre um pino liso em C. Determine a aceleração angular inicial da viga. Também determine as reações verticais e horizontais sobre a viga em A (considerada como um pino) nesse instante.
Passo 1
Iremos considerar a aceleração da gravidade .
Como temos que a viga rotaciona em torno de um ponto fixo A, temos:
No entanto, a viga está inicialmente em repouso, então:
Podemos ainda calcular o momento de inércia em torno de seu centro de massa:
Passo 2
Agora iremos aplicar o somatório de momentos em torno do ponto A com o auxílio da figura a seguir:
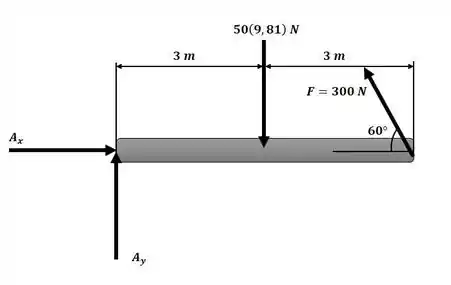
Passo 3
Agora podemos aplicar os somatórios de força nas direções normal e tangencial:
Resposta
Exercícios de Livros Relacionados
A haste esbelta de massa m e comprimento L está montada em um mandril que gira com o eixo da haste desalinhado em relação ao eixo z de rotação pelo ângulo β . Determine o momento fletor M O na base O
Se a placa triangular homogênea do Prob. 7/92 é liberada a partir do repouso na posição mostrada, determine o módulo da reação no mancal em A após a placa ter girado 90º.
A grande antena para rastreamento de satélite possui um momento de inércia I em relação a seu eixo z de simetria e um momento de inércia I o em relação a cada um dos eixos x e y . Determine a aceleraç
A placa possui uma massa de 3 kg e está soldada ao eixo vertical fixo, que gira na velocidade angular constante de 20 π r a d s . Calcule o momento M aplicado ao eixo pela placa devido ao desbalanceam
Se o mecanismo do Prob. 7/87 gira com uma velocidade angular constante maior do que a especificada na resposta para aquele problema, determine o momento de atrito M f que os pinos da articulação devem