Considerando as densidades de probabilidade ilustradas na figura acima, julgue os itens que se seguem a respeito dos momentos dessas distribuições.
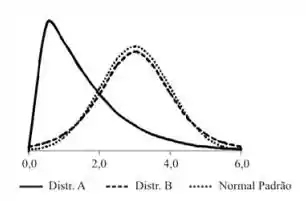
Julgue a curtose da distribuição B e a assimetria da distribuição A.
Passo 1
Se olharmos direitinho vemos que a distruibução B está abaixo da distribuição da Normal Padrão, o que quer dizer que ela está mais achatada que a Normal! Quando temos uma distribuição mais achatada que a Normal, dizemos que essa distribuição é platicúrtica e tem curtose negativa.
E quando a distribuição A, vemos que ela é assimétrica e está deslocada para a esquerda, e esse tipo de assimetria é classificada como assimetria positiva (ou à direita! – porque a cauda é mais longa na direita.)
Resposta
Distribuição A: assimétria positiva
Distribuição B: Platicúrtica