a) Seja “” uma v.a. normal com média “” e variância “”, e “” uma v.a. qui-quadrado .
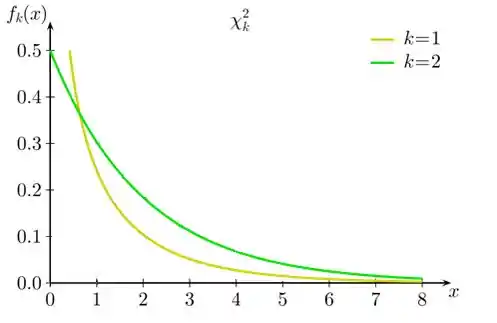
Se compararmos as curvas das funções densidade de probabilidade de uma distribuição qui-quadrado com “” graus de liberdade: e , qual destas duas curvas de variáveis aleatórias está mais próxima de ter um coeficiente de assimetria igual a zero, esboce em um mesmo gráfico as três curvas.
Passo 1
Vamos lembrar o significado dos valores que o coeficiente de assimetria pode assumir:
- Valores negativos: cauda do lado esquerdo da curva é maior que a do lado direito.
- Valores positivos: cauda do lado direito da curva é maior que a do lado esquerdo.
- Valores nulos: curva simétrica.
Então se a questão tá pedindo pra gente qual a curva está mais próxima de ter um coeficiente igual a zero, ela quer saber qual curva está mais próxima de ser simétrica!
Passo 2
Agora vamos lembrar a cara das curvas de uma distribuição qui-quadrado para diferentes graus de liberdade:
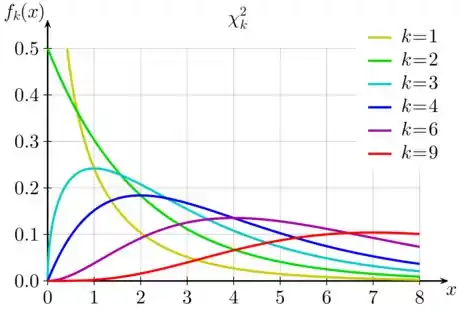
Podemos observar que as curvas tão ficando mais próximas de uma curva simétrica a medida que o grau de liberdade cresce.
A questão tá pedindo pra gente comparar uma curva com e outra com , e como vimos a tendência de simetria do gráfico, a com graus de liberdade está mais próxima de ser simétrica, ou seja, seu coeficiente de assimetria está mais próximo de zero!