Utilize os critérios das linhas para garantir convergência:
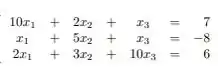
Passo 1
Um ponto importante em Jacobi-Richardson é que o critério das linhas será satisfeito se:
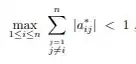
Na verdade, diferente de outros métodos, se nós conseguirmos garantir qualquer um, tipo, qualquer critério mesmo...Pasme, aí garantimos a convergência.

É isso mesmo, garantir um critério só já é sucesso.
Vemos que uma matriz qualquer A é estritamente diagonar dominante se a soma dos termos da linha for menor (em módulo) que o termo dominante da linha
Tendo o nosso sistema:
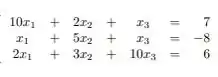
Existem duas maneiras de satisfazer o critério das linhas, primeiro é testar se a matriz é estritamente diagonal dominante e o outro falaremos no passo 2.
Vamos entender em termos de linhas e colunas:
Agora, testaremos se a matriz é estritamente dominante:
Apenas com esse critério, já garantimos que Jacobi-Richardson pode ser implementado!
Passo 2
Para calcular o critério das linhas propriamente dito, voltaremos láaaaaa pra nossa matriz:
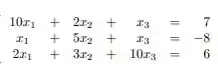
Faremos o seguinte, vamos pegar o termo dominante de cada linha (linha 1: , linha 2:, linha 3: ). E dividiremos os demais temos pelos termos dominantes:
Montando a função temos:
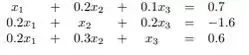
Mesmo não sendo necessário, já que garantimos a convergência no passo anterior, podemos calcular novamente os módulos assim:
Perceba que 0,5 foi o maior valor obtido, então é o nosso máximo, e o valor máximo deve ser sempre menor que 1. Então se 0,5
Resposta
Critério atendido