Considere a treliça abaixo como isostática. Calcule o valor dos esforços normais de todas as barras, utilizando o método dos nós, indicando o correspondente em KN para cada barra. Na questão, para cada realização do DCL dos nós, será descontada uma pontuação de 0,2.
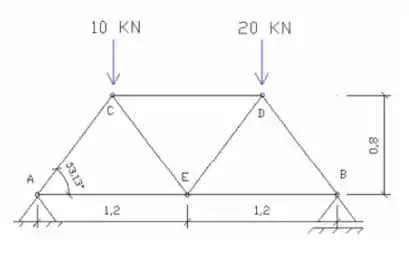
Passo 1
Como o nosso enunciado já diz, precisaremos determinar os esforços em cada barra! Certo?Mais ou menos né... Pois, dessa vez o professor foi um pouco mais maldoso!
Nessa prova o intuito dele, era testar se os alunos conseguiriam realizar a separação de cada nó sem o auxílio dos desenhos, ou seja sem o DCL (Diagrama de Corpo Livre)!
Só que ele não contava com a gente, rs e vamos ver que é possível fazer o exercício sem os DCL’s.Então bora lá usar o método dos nós sem os DCL’s , tenho certeza que a gente consegue...

Primeiro precisamos vamos verificar quais são os valores das reações dos apoios! Antes vamos estipular o seguinte, só entre nós, se as forças estiverem para esquerda ou para baixo elas vão ganhar um sinal negativo, se as forças estiverem para direita ou para cima , vão ganhar um sinal positivo ok? Isso vai salvar muito nossa vida!No nó A tempos um apoio de segundo gênero, dessa forma teremos uma força na horizontal e uma na vertical (Ax e Ay) e no nó B temos um apoio de primeiro gênero, com uma única reação na vertical (By).Dessa forma, podemos agora determinar o valor das reações.
Somatório dos momentos em relação ao ponto A:
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 2
Vamos pensar no isolamento do ponto A na treliça;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 3
Próximo nó que podemos isolar é o nó C;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 4
Próximo nó que podemos isolar é o nó E;
Somatório das forças verticais iguais a zero:
Somatório das forças horizontais iguais a zero:
Passo 5
Próximo nó que podemos isolar é o nó D;
Somatório das forças horizontais iguais a zero:
Passo 6
Próximo nó que podemos isolar é o nó B;
Somatório das forças horizontais iguais a zero:
Resposta
Todas as forças positivas são forças de tração e todas as forças negativas são forças de compressão.