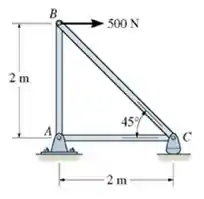
Determine a força em cada elemento da treliça mostrada na Figura abaixo. Indique se os elementos estão sobre tração ou compressão.
Passo 1
Bom, precisamos começar entendendo o enunciado,
Para esse exercício precisaremos calcular todas as reações a fim de entender quais elementos estão sobre tração e quais sobre compressão. Além disso, precisamos entender quais são as reações nos apoios.
No apoio no ponto A existem uma reação Ax e uma reação Ay, visto que temos um apoio de segundo gênero.
Já no apoio no ponto C existe apenas uma reação Cy, visto que temos um apoio de primeiro gênero.
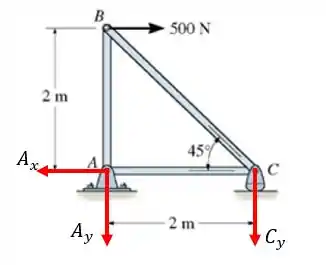
Passo 2
Agora é a hora calcular as reações de apoio.

Vamos usar as condições para a treliça estar em equilíbrio, são elas;
Somatório dos momentos em relação ao ponto C igual a zero. Aqui vamos fazer o somatório dos momentos em relação à para podermos eliminar tanto o termo quanto o termo .
Somatório das forças verticais igual a zero:
Somatório das forças horizontais igual a zero:
Passo 3
Agora podemos analisar cada Nó da treliça.
Vamos começar analisando o nó A;
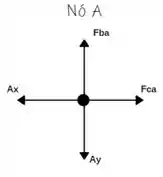
Somatório das forças horizontais igual a zero:
Somatório das forças verticais igual a zero:
;
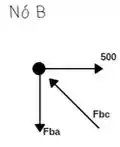
Somatório das forças horizontais igual a zero:
Somatório das forças verticais igual a zero:
Agora vamos analisar o nó C;
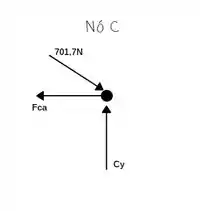
Somatório das forças horizontais igual a zero:
Somatório das forças verticais igual a zero:
Com todas as reações computadas, chegamos a seguinte resposta:
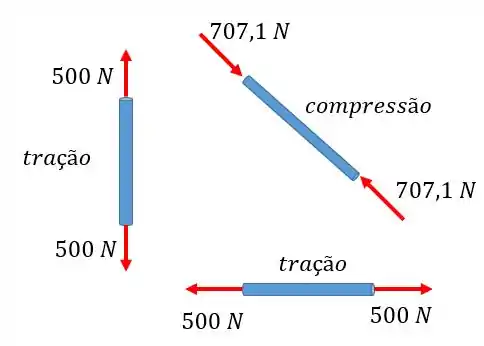
Resposta
Barra AC (Tração)Barra AB (Tração)Barra BC (Compressão)