Um certo sistema, ao ser perturbado com uma entrada degrau unitária, apresenta a seguinte curva de reação
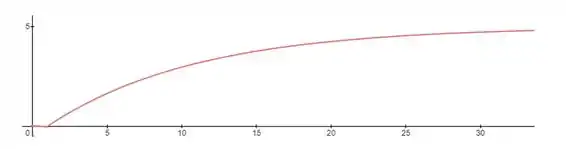
Projete um controlador PID para esse sistema utilizando os parâmetros de Zielger-Nichols de malha aberta.
Passo 1
Vamos começar encondtrando a função FOPDT que aproxima o sistema:
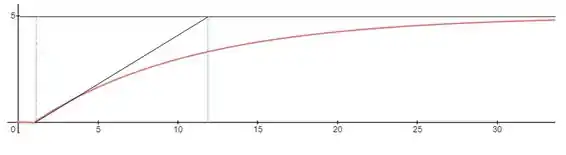
Pela figura acima, podemos ver que o ponto onde a tangente cruza o valor inicial é aproximadamente , portanto:
Já o ponto que a tangente cruz a linha do falor final da resposta é aproximadamente 12, portanto:
E o ganho do sistema é a variação da resposta dividida pela amplitude do degrau, a variação da resposta nós podemos estimar como 5, e como o degrau foi um degrau unitário, o ganho é simplesmente:
Sendo assim, a nossa aproximação ficará:
Passo 2
Para projetar nosso controlador PID precisamos encontrar três parâmetros: , e . Podemos encontrar as correlações para esses parâmetros na tabela de Ziegler Nichols para malha aberta

Como nosso controlador é PID, vamos usar a última linha para definir nossos parâmetros. Então:
A função de transferência do controlador será então: