Considere o sistema mostrado na figura abaixo:
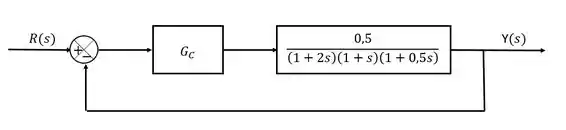
Calcule os ajustes de um PID para esse sistema utilizando o método de Ziegler-Nichols de malha fechada.
Passo 1
Para aplicar o método de ZN em malha fechada, é preciso determinar o ganho e período final do sistema. Para isso, usaremos o método da substituição direta.
A função de transferência dessa malha será:
Onde é a função de transferência do processo (segundo bloco). O denominador dessa função de transferência é a nossa equação característica.
Para fazer esse método, primeiramente consideramos o controlador como puramente proporcional e em seguida encontramos o ganho último pelo método da substituição direta:
Portanto:
Passo 2
Vamos então aplicar o método da substituição direta:
Devemos agora igualar tanto a parte real como a parte imaginária a :
Da parte imaginária temos:
Substituindo na parte real:
Além disso, sabendo que:
Passo 3
Com os valores de e calculados, é possível fazer a sintonia pelo método de ZN de malha fechada. Usaremos as correlações da tabela abaixo:
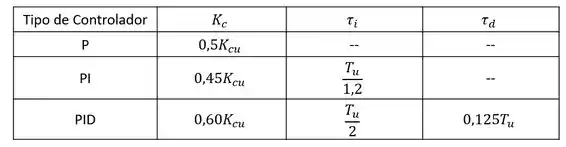
Como queremos um controlador PID, usaremos as correlações da última linha.
Portanto, a função de transferência do controlador será: