Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Métodos de Ziegler-Nichols

Ver Teoria
Exercício 41235678

Enunciado

Um sistema possui os seguintes valores para ganho ganho e período final:

K C u = 2,5

T u = 0,6

Sintonnize um controlador P, PI e PID para esse sistema usando as correlações de decaimento ¼ de Ziegler-NIchols em malha fechada.

Passo 1

Para fazer as sintonizações, usaremos a tabela abaixa que apresenta as correlações de Ziegler-Nichols em malha fechada:

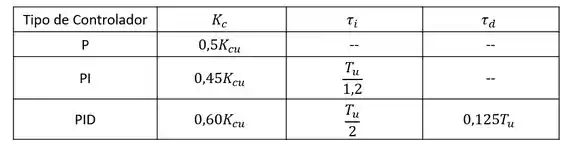
Passo 2

Um controlador do tipo P tem apenas um parâmetro a ser sintonizado:

G C s = K C

Usando a correlação da tabela:

K C = 0,5 K C u = 0,5 * 2,5 = 1,25

Portanto

G C = 1,25

Passo 3

Para um controlador PI, teremos que calcular dois parâmetros:

G C s = K C 1 + 1 τ i s

Usando as correlações da tabela:

K C = 0 , 4 5 K C u = 0 , 4 5 * 2,5 = 1,125

τ i = T u 1,2 = 0,6 1,2 = 0,5

A função de transferência do controlador será então:

G C s = 1,125 1 + 1 0,5 s

Passo 4

Por último, um controlador PID precisa que três parâmetros sejam sintonizados:

G C s = K C 1 + 1 τ 1 s + τ d s

Seguindo as correlações de Ziegler-Nichols para um controlador PID:

K C = 0 , 60 K C u = 0 , 60 * 2,5 = 1 , 5

τ i = T u 2 = 0,6 2 = 0 , 3

τ d = 0,125 T u = 0,125 * 0,6 = 0 , 07 5

O controlador será então:

G C s = 1,5 1 + 1 0,3 s + 0,07 5 s

Resposta

Controlador P:

G C = 1 , 25

Controlador PI:

G C s = 1,125 1 + 1 0,5 s

Controlador PID:

G C s = 1,5 1 + 1 0,3 s + 0,075 s