Um certo sistema, ao ser perturbado com uma entrada degrau unitária, apresenta a seguinte curva de reação
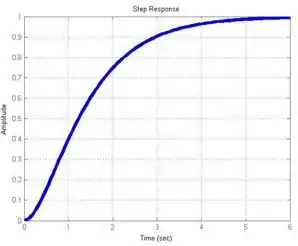
Projete um controlador PID para esse sistema utilizando os parâmetros de Zielger-Nichols de malha aberta.
Passo 1
Para definir os parâmetros do controlador, precisamos aproximar o sistema da curva a uma função de transferência de primeira ordem com tempo morto (FOPDT). Para isso, precisamos traçar a maior tangente com maior inclinação possível no gráfico do enunciado.
Essa tangente, será mais ou menos assim (não presisa ser extao, lembre-se, é uma aproximação):
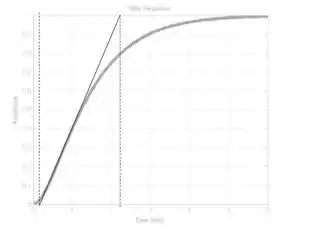
Passo 2
Agora precisamos encontrar os parâmetros da função de transferência de primeira ordem com tempo morto:
O ganho , é a variação total da saída. Como a saída variou de até , o ganho é .
O tempo morto, , é a distância entre o início da curva e o ponto onde a reta tangente que a nós traçamos cruza o valor inicial da respota.
Pelo nosso esboço, podemos estimar o ponto em que isso acontece como mais ou menos . Sendo assim:
Por fim, a constante de tempo, , é aproximada pela diferença entre o tempo que a reta tangente cruza o valor final e o tempo que a reta tangente cruza o valor inicial. Portanto:
Sendo assim, nossa função de primeira ordem com tempo morto (FOPDT) aproximada ficou com a seguinte cara:
Passo 3
Para projetar nosso PID precisamos encontrar três parâmetros: , e . Podemos encontrar as correlações para esses três parâmetros na tabela de Ziegler Nichols para malha aberta

Como nosso controlador é PID, vamos usar a última linha para definir nossos parâmetros. Então:
A função de transferência do controlador será então: