Um carro está a uma velocidade constante de em uma zona escolar. Um carro de polícia parte do repouso assim que o velocista passa por ele e acelera a uma taxa constante de . A que velocidade o carro de polícia está viajando quando está a atrás do velocista?

Essa é pra finalizar com chave de ouro, ein !

Antes vamos tentar desenhar o que está acontecendo:

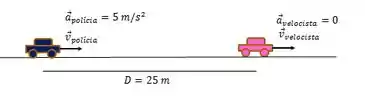
A velocidade do velocista é constante, portanto não há aceleração para ele, ok? Se o movimento é uniforme, podemos usar a equação horária da posição

O policial está acelerando, então seu movimento é uniformemente variado e sua posição é dada por:

Existem algumas informações no enunciado que temos que deduzir que nem Sherlock Holms. Fica ligado nessas palavras-chave que aparecem em muitos exercícios.

Primeiro ele diz que o carro da polícia parte do repouso, então

depois diz que o policial começa a acelerar quando o velocista passa por ele, ou seja, quando suas posições são as mesmas

Opa, coloquei uma informação a mais alí! além das posições iniciais serem as mesmas, também posso definir que ele partem da posição , que é quando vamos começar a marcar a distância entre eles.

Agora acrescentando essas informações nas equações horárias do policial e do velocista, teremos para o velocista

como foi falado que a velocidade do velocista é constante e igual a , podemos substituir

e para o policial

também é dito que a aceleração do policial é de , substituindo nessa equação

Sabemos que a distância entre os dois carros é de , então a posição do velocista menos a posição do policial deve ser igual à distância dada:

vamos substituir as equações que encontramos para o velocista e para o policial nessa distância

Multiplicamos todos os termos por para tirar aquela fração

Para simplificar, vamos dividir tudo por

E agora vamos enviar para o outro lado da igualdade o termo com sinal oposto:

Quando aparece uma equação do segundo grau, usamos a fórmula quadrática (lembra do Baskara? haha)

Olhando na equação, o termo que está acompanhando é conhecido como , o que está com o é chamado de enquanto o que está sozinho é chamado de

Substituindo:

Temos dois valores para

Agora que achamos o tempo fica fácil achar a velocidade do policial, certo?