Um bloco de massa está sendo puxado por uma corda. O módulo da força necessária para movimentar o bloco é dado por:
Onde e é chamado de coeficiente de atrito e e é chamada de aceleração da gravidade.
Determine o ângulo e a massa máxima no qual a força seja equivalente a
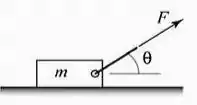
Passo 1
Aqui temos uma questão de subplot, a questão em si pode ser resolvida de diversas formas, porém o subplot se torna uma alternativa mais simples.
O subplot se torna uma alternativa simples pois estamos procurando um conjunto de valores de ângulo e massa pelo o qual a força exercida para movimentar o bloco seja equivalente a .
Como o subplot conseguimos colocar diversos gráficos em uma mesma janela, analisar o gráfico para obter essa informação fica muito mais simples.
Para resolução do problema precisamos criar dois vetores para fazer a função dada no problema variar e encontrarmos esses valores.
O primeiro vetor é o vetor de ângulo que vamos variar de 0 até .
Porque quando passamos de pelo desenho vamos puxar o bloquinho na direção contrária.
E a massa vai variar de 0 até 20 kg, pois um bloco de mais de 21 kg não parece fisicamente muito normal de se encontrar sendo puxado por uma cordinha, belezinha?
Para finalizar vamos calcular a função sob esses vetores e vamos finalizar imprimindo um graficozinho para melhor analisar e obter a nossa resposta.
Sendo assim, o algoritmo para a resolução do problema se torna:
1-Implementação da entrada de dados.
2-Criação dos vetores Massa e Ângulo.
3-Cálculo da força.
4-plotagem utilizando o subplot.
Passo 2
Agora que criamos o algoritmo vamos implementá-los no Matlab.
Primeiramente vamos implementar a entrada de dados dentro do Matlab.
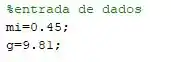
Agora que já implementamos a entrada de dados, o segundo passo é implementar os vetores de massa e ângulo.
O vetor de massa vamos implementar com uma variação de 1, para não ficar muito ponto e o cálculo não ficar pesado, arbitrariamente vamos chamar essa variável de M.
![]()
Agora vamos implementar os valores de teta, com o teta variando de 0 até , gostaríamos que tivesse a mesma quantidade de pontos que a variável M.
Para isso definimos o incremento como sendo:
Fazendo com que o vetor teta tenha 20 elementos e resultando em:
![]()
Agora que implementamos os valores dos ângulos vamos calcular a função desejada:
![]()
Lembrando que estamos realizando uma operação elemento a elemento do vetor, como nós temos um vetor M sendo dividido pelo vetor temos que colocar o ponto “.” Para indicar a operação elemento a elemento.
Passo 3
Agora vamos iniciar o plot, para isso vamos primeiramente falar do subplot.
Para criar o precisamos lembrar de sua sintaxe, primeiramente precisamos lembrar que o tem 3 argumentos na sua função.
O primeiro argumento da função vai falar quantas colunas o vai ter, aqui temos apenas dois gráficos logo duas colunas é suficiente.
Como temos 2 gráficos e colocamos duas colunas no nosso subplot o número de linhas se torna 1, que é o nosso segundo argumento. Sendo assim o subplot fica:
Vou escolher arbitrariamente que o primeiro gráfico seja o do teta então o terceiro argumento do subplot fica 1 e vou indicar que nele irá localizar o plot da função .
e agora iremos chamar a função onde iremos indicar no primeiro argumento o eixo e no segundo argumento a variável dependente.
![]()
Agora vamos nomear os eixos para ficar algo mais organizado e para isso iremos precisar de duas funções. A função e a outra se chama a .
Para nomear os eixos precisa apenas fazer o seguinte procedimento:
Ou seja, precisamos apenas chamar a função, colocar o igual e escrever entre aspas simples o nome do eixo.
Na realidade estamos anexando um string aos eixos.
Analogamente vamos imprimir na segunda janela do subplot, então seu subplot fica:

Digitando tudo certinho seu código fica:

Passo 4
Executando o código irá obter os seguintes gráficos.

E analisando as curvas acima podemos verificar que os valores para obter uma força de 100 N são aproximadamente teta=1,3 raianos e um valor de Massa igual a 17 kg.
Passo 5
Resposta
Ei, a resposta está no passo a passo :)