Elabore em Matlab uma rotina que consiga plotar os gráficos das funções seno, cosseno e tangente variando de até em uma única janela gráfica.
Passo 1
A questão em si é uma questão simples da aplicação da ferramenta subplot, para isso precisamos escrever o código para calcular as funções e depois gerar os gráficos em uma única janela gráfica.
Primeiramente, vamos escrever o algoritmo para a resolução do problema.
1 - Entrada de dados: criação do vetor ângulo
2 - Cálculo funções do problema
3 -Criação dos gráficos com o subplot
Passo 2
Uma vez que criamos o algoritmo iremos agora implementar o código no Matlab.
Primeiramente iremos criar o vetor ângulo:
Agora iremos calcular as funções no Matlab:
Uma vez que calculamos as funções, iremos criar os plots e em seguida iremos organizá-los:
Vamos utilizar o subplot e criar uma matriz coluna, pois temos 3 funções e cada um irá retornar um gráfico diferente, sendo assim o gráfico do cosseno fica:
O seno por sua vez irá ocupar o segundo gráfico, então:
E finalmente terceiro gráfico será ocupado pela tangente
Sendo assim seu código irá se tornar:

Passo 3
Executando o código iremos obter o seguinte gráfico:
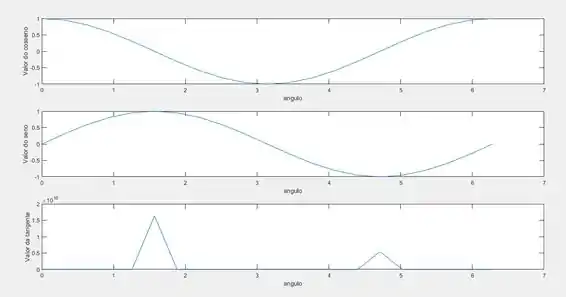
Aqui podemos notar que em locais onde o cosseno é zero a tangente ela assume valores tendendo ao infinito como se esperado pois por definição a tangente é inversamente proporcional ao cosseno, ou seja quanto mais o cosseno diminui mais a tangente cresce.
Resposta
Ei, a resposta está no passo a passo :)