O deslocamento de uma borda é o nome dado a um defeito em uma amostra de cristal onde um grupo de átomos do cristal se desprende da estrutura cristalina. As componentes de tensão em volta da porção deslocada são dadas por:
Onde é o modulo de cisalhamento, é o módulo do vetor de Burgers e é a razão de Poisson. Plote as componentes de tensão devido ao deslocamento da borda de alumínio onde as tensões serão plotadas entre o intervalo:
Sendo:
Passo 1
Aqui é uma questão de plotagem onde iremos utilizar a função para uma melhor visualização das figuras.
A visualização se torna melhor pois conseguimos incluir as duas informações gráficas em uma mesma janela, tornando possível a realização de comparações para análises mais aprofundadas dos gráficos.
Então para a criação do precisamos criar o vetor para calcular as funções dentro desse intervalo desejado e depois disso imprimir o gráfico em uma janela gráfica utilizando a janela
Para criar o precisamos lembrar de sua sintaxe, primeiramente precisamos lembrar que o tem 3 argumentos na sua função.
O primeiro argumento da função vai falar quantas colunas o vai ter, aqui temos apenas dois gráficos logo duas colunas é suficiente.
Como temos 2 gráficos e colocamos duas colunas no nosso subplot o número de linhas se torna 1, que é o nosso segundo argumento. Sendo assim o subplot fica:
O terceiro índice é a numeração do gráfico que será explorado no final do exercício.
Sendo assim, o algoritmo se torna:
1-Criação do vetor e implementação dos dados do problema
2-cálculo das funções do problema
3-Implementação dos gráficos com o subplot e organização do mesmo.
Passo 2
Agora que montamos o nosso algoritmo vamos transformá-lo em um código do Matlab.
Primeiramente vamos criar o vetor arbitrariamente vou colocar um incremento de .
Agora vamos implementar os demais dados do problema.
Agora precisamos implementar as funções do problema:
Agora que criamos as funções vamos implementar os subplots.
Vou escolher arbitrariamente que o primeiro gráfico seja o do sigma, então o terceiro argumento do subplot fica 1 e vou indicar que nele irá localizar o plot da função sigma.
e agora iremos chamar a função onde iremos indicar no primeiro argumento o eixo e no segundo argumento a variável dependente.
Organizando os gráficos nomeando os eixos com a função , temos:
Analogamente vamos imprimir na segunda janela do subplot a função , então seu subplot fica:
Digitando tudo certinho seu código fica:

Executando o código temos o seguinte gráfico.
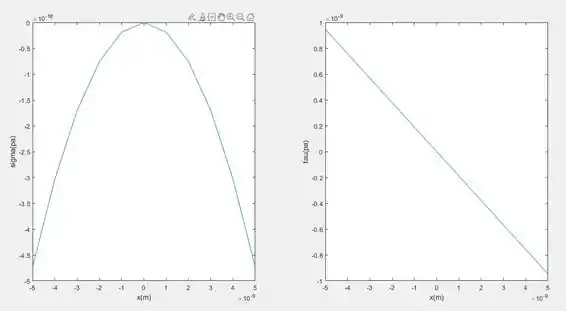
Resposta
Ei, a resposta está no passo a passo :)