Uma partícula é lançada obliquamente no vácuo, a em relação ao eixo X, suposto fixo no solo, e com uma elevação de. Construa uma representação gráfica revelando a trajetória dessa partícula, ao longo dos três eixos.
Para esse lançamento oblíquo em coordenadas esféricas utilize as seguintes equações:
Velocidades iniciais:
Deslocamento:
Passo 1
A questão pede para elaborarmos um programa em Matlab que a partir de dados iniciais possamos prever toda a dinâmica de uma partícula no vácuo em um espaço tridimensional.
A ideia aqui é realizar o subplot e plotar as curvas nos X,Y e Z e finalizar com uma curva 3d de linhas, ok?
Primeiramente iremos criar o algoritmo:
1-Entrada de dados
2-Criação e cálculo das funções
3-Finalização com a saída gráfica.
Uma vez que o algoritmo esteja pronto, vamos para o próximo passo.
Passo 2
Uma vez que criamos o algoritmo iremos agora implementar o código no Matlab.
Primeiramente, temos que implementar a entrada de dados:
Agora vamos criar o vetor tempo:
E agora iremos implementar as funções:
Passo 3
E vamos finalizar o código inserindo os subplots. Como temos 4 gráficos (três variáveis espaciais + a superfície 3D) para plotar, vamos criar um subplot para plotar as três variáveis espaciais e depois utilizaremos um comando figure para plotar a curva 3D.
O comando subplot divide a janela gráfica em uma matriz de gráficos, pra casos como essa questão, que nós temos vários gráficos. A sintaxe do subplot funciona da seguinte forma: são 3 argumentos: o primeiro diz quantas linhas essa matriz gráfica vai ter; o segundo argumento é o número de colunas; e o terceiro indica a ordem dos gráficos no subplot.
Como temos 3 gráficos (), vamos fazer uma matriz com 3 linhas e 1 coluna. E o gráfico em vai ser o primeiro, então o argumento do subplot fica .
E nosso segundo gráfico se torna:
O terceiro gráfico irá se tornar:
E por último iremos plotar a superfície 3D. Daí como os gráficos acima foram plotados numa figura só, o gráfico em 3D vai ser a segunda figura.
Implementando tudo corretamente iremos gerar a seguinte rotina:
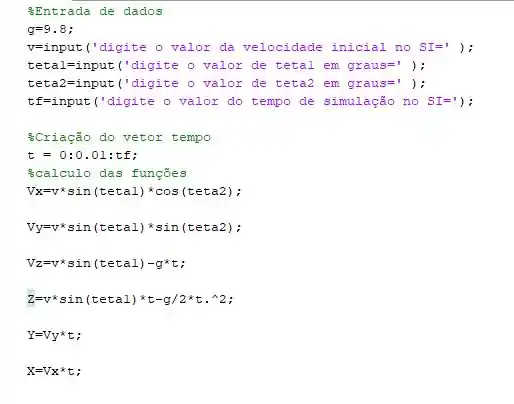

Passo 4
Executando o código iremos obter os seguintes gráficos:
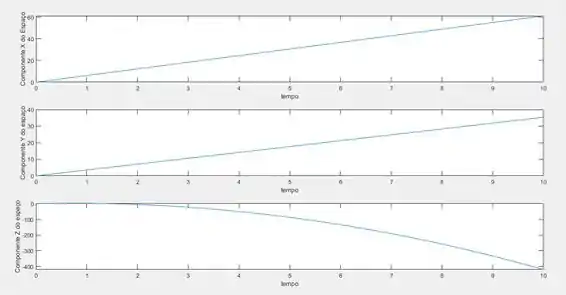
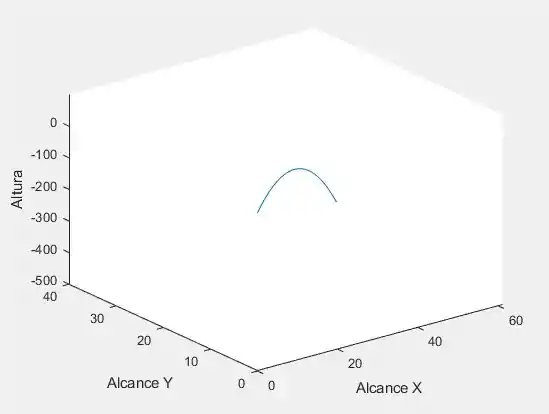
Resposta
Ei, a resposta está no passo a passo :)