O mecanismo constituído de uma manivela de êmbolo é usado em muitas aplicações na engenharia. No mecanismo mostrado a seguir, a manivela gira em uma velocidade constante de 50 rads/s.

Calcule e esboce a posição, a velocidade e a aceleração do êmbolo para uma revolução da manivela. Construa três gráficos na mesma janela de saída com todas as unidades no SI.
Utilize as seguintes equações para os cálculos:
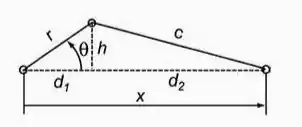
Posições:
Velocidades:
Aceleração:
Passo 1
A questão pede para elaborarmos um programa em Matlab que a partir de dados iniciais possamos prever toda a dinâmica do mecanismo apresentado na questão.
A ideia aqui é criar um vetor de tempo e calcular as variáveis cinemáticas do mecanismo e criar um subplot para plotar todas em uma única janela gráfica.
Primeiramente iremos criar o algoritmo:
1-Entrada de dados
2-Criação e cálculo das funções
3-Finalização com a saída gráfica.
Uma vez que o algoritmo esteja pronto, vamos para o próximo passo.
Passo 2
Uma vez que criamos o algoritmo iremos agora implementar o código no Matlab.
Primeiramente, temos que implementar a entrada de dados:
Agora vamos criar o vetor tempo:
E agora iremos implementar as funções:
E vamos finalizar o código inserindo os subplots, como temos 3 gráficos logo iremos gerar uma janela gráfica com 3 linhas e uma coluna, sendo assim o primeiro gráfico se torna:
E nosso segundo gráfico se torna:
O terceiro gráfico irá se tornar:
Implementando tudo corretamente iremos gerar a seguinte rotina:

Passo 3
Executando o código iremos obter os seguintes gráficos:
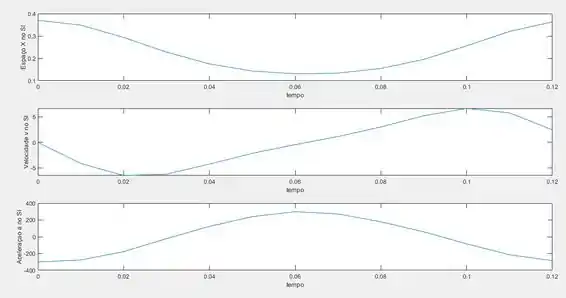
Resposta
Ei, a resposta está no passo a passo :)