UTFPR, Sem Campus, Cálculo Diferencial e Integral 3, AV3 - 2022.2, Questão 5
Encontre a forma polar no número complexo e represente (um esboço) este número no plano complexo.
Passo 1
Oiiie, tudo bem?
O enunciado nos dá um número complexo da forma
e, pede para representarmos esse número em sua forma polar, ou seja, representá-lo usando a relação
Mas quem são e ? São o módulo e o ângulo no plano complexo dado por
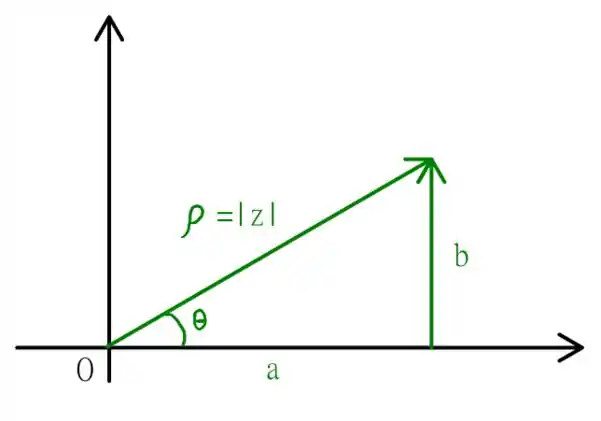
Em que
aqui, chamei , o conjugado de . Mas antes de qualquer coisa, vamos precisar deixar o nosso número complexo no formato usual! Vem comigo!
Passo 2
Temos o seguinte número complexo
Para deixá-lo no formato , vamos multiplicar o denominador e o numerador pelo conjugado de , ou seja
Como temos que , podemos simplificar a expressão acima para obter:
Achamos o número complexo na sua forma usual! E o seu conjugado é:
Agora podemos obter o módulo com
Podemos realizar a soma acima para obter:
+3
Beleza! Vamos calcular o ângulo agora! Vem comigo!
Passo 3
Nós obtemos que o nosso número tem a forma
Portanto, temos que , pelo triângulo retângulo no passo , podemos notar que
Ou seja, temos que em coordenadas polares, nosso número complexo é:
E, seu esboço no plano complexo é simplesmente:
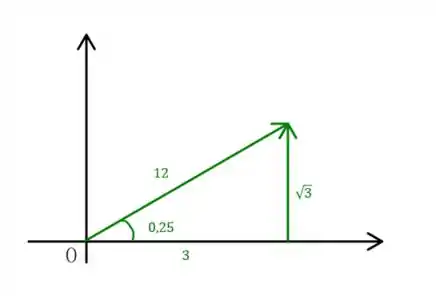
A questão foi isso! Te vejo na próxima! Tchauzinho!