Qual será o valor de ?
Dado que e
Passo 1
Já sabemos que
Depois disso, vimos que a gente repete a mesma sequência de números do
Se somarmos esses valores, teremos
Isso mesmo, de 4 em 4 essa soma vai dando zero.
O último elemento dessa sequência é
Maaas, pera aí
Vamos refletir,
Ou seja,
O último elemento da série vai ser o
Beleza, mas no que isso adianta a gente?
Passo 2
A nossa série está da seguinte forma
No entanto toda essa parte aqui, se anula
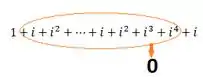
Portanto, toda essa soma será igual ao que sobrou ali, portanto