O desembaçador de pára-brisa de carros funciona jogando ar quente na superfície interna do pára-brisa. Para evitar a condensação de vapor d’água nesta superfície, a temperatura do ar e o coeficiente convectivo na superfície devem ser grandes o suficiente para manter uma temperatura na superfície , que seja, pelo menos, superior ao ponto de orvalho .
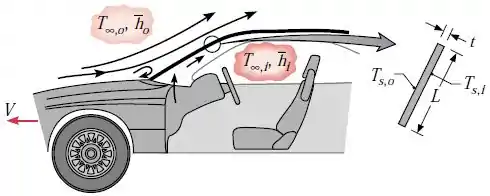
Considere um pára-brisa com comprimento e espessura , e condições de direção nas quais o carro se desloca a uma velocidade em um ambiente a .
Com base em experimentos de laboratório efetuados em um modelo do carro, sabe-se que o coeficiente de convecção médio na superfície externa do pára-brisa é correlacionado por uma expressão com a forma
, onde .
As propriedades do ar ambiente podem ser aproximadas por , e . Se e , qual é o menor valor de requerido para evitar a condensação na superfície interna?
Passo 1
O menor valor de será aquele para o qual a temperatura na superfície interna é igual à temperatura no ponto de orvalho, ou seja, .
Repare que o sistema dado pelo problema pode ser representado pelo seguinte circuito térmico:
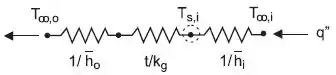
Como não temos o fluxo de calor no problema, podemos escolher um ponto e igualar o fluxo de calor calculado pelos dois lados desse ponto.
Nesse caso, vamos escolher a superfície interna do vidro, a qual sabemos a temperatura .
Dessa forma, a resistência térmica por unidade de área e o fluxo de calor à direita da superfície interna é dada por:
Do lado esquerdo, a resistência térmica por unidade de área e o fluxo de calor são dados por:
Onde é a condutividade térmica do vidro que, de acordo com a tabela A.3 do Incropera, vale .
Igualando as duas expressões do fluxo de calor, teremos:
Dessa expressão, a única coisa que não temos é o coeficiente convectivo externo . Então vamos trabalhar nesse cara.
Passo 2
De acordo com o problema, o coeficiente de convecção médio na superfície externa do pára-brisa é correlacionado por uma expressão com a forma
Por definição, o número de Nusselt médio é dado por:
Igualando as duas expressões:
Antes de continuarmos, vamos calcular esse número de Reynolds.
Passo 3
O número de Reynolds é dado por:
Onde:
Logo:
Passo 4
Voltando ao cálculo de :
Onde:
Substituindo os valores:
Agora podemos finalmente calcular ! Eu ouvi “amém”?! \o/
Passo 5
Voltando à expressão que encontramos no Passo 1:
Vamos reorganizar esse cada pra encontrar :
Onde:
Dessa forma:
