Ar forçado a e é usado para resfriar elementos eletrônicos em uma placa de circuito. Um desses elementos é um chip, que mede por , localizado a da aresta frontal da placa.
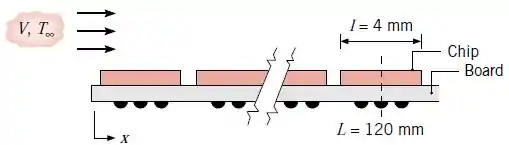
Experimentos revelaram que o escoamento sobre a placa é perturbado pelos elementos e que a transferência de calor por convecção é relacionada por uma expressão com a forma
Estime a temperatura superficial do chip se ele estiver dissipando .
Passo 1
Vamos nessa!
Podemos calcular a temperatura superficial do chip através da Lei de Resfriamento de Newton:
A única coisa que não temos dessa equação é justamente o coeficiente convectivo. Então vamos calcular esse cara.
Pra isso, antes de qualquer coisa, temos que encontrar as propriedades do ar que vamos precisar. Geralmente, nesse caso, a gente pega os dados a partir da média das temperaturas entre a da superfície e a de corrente livre .
Opa! Mas é justamente o cara que queremos calcular, como fazemos nesse caso?
Nesse caso, vamos ter que chutar um valor para , mas não pode ser nada absurdo aqui, beleza? Procure chutar um valor que vá ajudar na hora de olhar nas tabelas do livro.
Vamos chutar aqui um valor de . Fazendo isso, teremos:
Sendo assim, buscando os dados para , teremos o seguinte:
Agora podemos seguir em frente. :)
Passo 2
Pra calcularmos o coeficiente convectivo, vamos usar a equação de Nusselt que o problema nos deu:
Por definição:
Dessa forma:
Onde:
Substituindo os valores:
Passo 3
Agora podemos calcular a temperatura na superfície:
Onde:
Substituindo os valores:
Opa! O valor que encontramos foi bem próximo do valor que chutamos no início do problema, então esse foi um bom chute.
Caso os valores fossem muito distintos, a boa seria refazer os cálculos para um novo chute, agora mais próximo do valor que teríamos encontrado.