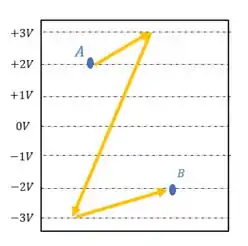
A figura mostra a configuração das equipotenciais (linhas tracejadas) de um campo eletrostático. Uma carga de deve ser deslocada entre os pontos e , pela trajetória indicada por traço cheio, na figura. O trabalho realizado pelas forças eletrostáticas no deslocamento de para é de:
Passo 1
Pessoal bonito, vamos lembrar de uma coisa MUITO IMPORTANTE! O trabalho não depende da trajetória, apenas do potencial final e inicial da trajetória.
Nesse caso, o ponto inicial é o ponto e o ponto final é o .
Passo 2
Podemos perceber que o ponto está sob uma linha de potencial igual a , então sabemos que o potencial inicial é:
Enquanto o ponto final está sob uma linha de potencial igual a , então o sabemos que o potencial final é:
A diferença de potencial elétrico é igual a:
Substituindo os valores que já encontramos pela figura:
Resultando em:
Passo 3
E como relacionamos a diferença de potencial e o trabalho realizado para levar a carga ? Simples, através da fórmula:
Não esqueçam daquele sinalzinho de menos alí hem. O enunciado já nos deu o valor da carga :
E já calculamos a diferença de potencial ,
Como precisamos do , vamos multiplicar tudo por :
A multiplicação entre dois números negativos resulta em um número positivo:
Logo, vamos aplicar esses valores na equação:
Rapidinho achamos a resposta, não foi? Você já está ficando craque, mas vamos fazer mais exercícios para fixar bem e nunca mais esquecer!
Resposta
c)