Nos quatro vértices de um quadrado são fixadas quatro cargas e , alternadamente. Considere o campo elétrico e o potencial no centro do quadrado como e , respectivamente. Assinale a opção correta:
- maior que zero e igual a zero.
- menor que zero e igual a zero
- igual a zero e diferente de zero
- e iguais a zero
- e diferentes de zero
Passo 1
Vamos primeiro desenhar o que ele falou no enunciado:
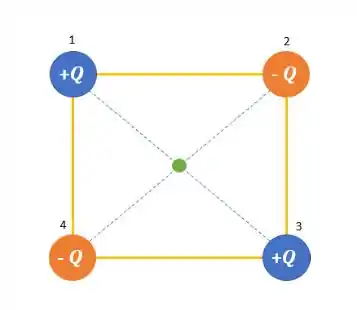
Sendo que marcamos o centro do quadrado com aquele pontinho verde.
Passo 2
Quem vai ser o campo elétrico no centro do quadrado? A soma de todos os campos elétricos gerados por todas as cargas, então:
Só tomem cuidado porque o campo elétrico é uma grandeza vetorial, então temos que levar em consideração a direção e sentido de cada um deles. Vamos voltar a falar disso mais na frente, por enquanto guardem essa informação 😊
Assim também faremos com o potencial elétrico:
Já com o potencial não precisamos nos preocupar, é uma grandeza escalar. Então é só somar todo mundo mesmo e pronto.
Quais são as expressões para calcular o campo elétrico e potencial de cada carga? São essas aqui:
Passo 3
Vamos calcular para cada uma das cargas essas informações. Presta atenção em uma coisa: todas as cargas estão a mesma distância do centro! Vamos chamar essa distância de :
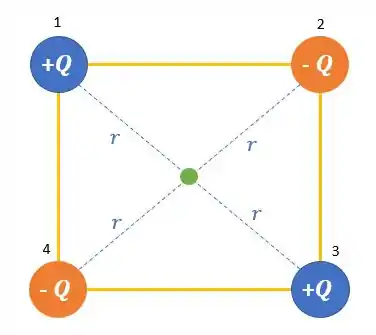
Para a primeira carga que é positiva, vamos substituir os valores:
Para a segunda carga que é negativa, vamos substituir os valores:
Veja que levamos em consideração os sinais das cargas!
Vamos fazer o mesmo para a carga que é positiva:
E por último para a quarta carga que é negativa:
Passo 4
Vamos somar todas as parcelas do campo elétrico, como dissemos no início? Vou te ajudar!
Lembra que falei que o campo elétrico é um vetor? Então, precisamos pegar os pares de cargas que fazem o campo ficar na mesma direção, no caso com e com .
Olhando primeiro para e
Agora para e
Então, substituindo as parcelas:
Concorda comigo que as parcelas positivas se cancelam com as parcelas negativas? Isso acontece, pois as parcelas são iguais, mas com sinais opostos!
Passo 5
Vamos repetir a soma para o potencial elétrico de cada carga!
Então, substituindo as parcelas:
Mais uma vez as parcelas positivas se cancelam com as parcelas negativas, pois as parcelas são iguais, mas com sinais opostos!
Passo 6
Chegamos na resposta final, que tanto o campo elétrico total quanto o potencial elétrico total é igual a zero!
Resposta
d) e iguais a zero