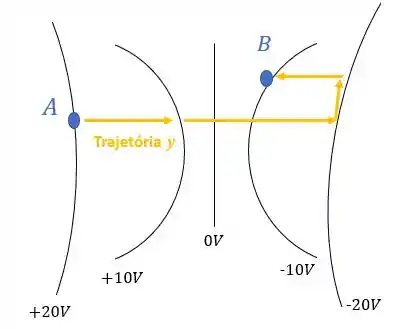
A figura representa algumas superfícies equipotenciais de um campo eletrostático e os valores dos potenciais correspondentes. O trabalho realizado pelo campo para levar uma carga de do ponto ao ponto , através da trajetória , vale, em Joules:
Passo 1
Pessoal bonito, vamos lembrar de uma coisa MUITO IMPORTANTE! O trabalho não depende da trajetória, apenas do potencial final e inicial da trajetória.
Nesse caso, o ponto inicial é o ponto e o ponto final é o .
Passo 2
Podemos perceber que o ponto está sob uma linha de potencial igual a , então sabemos que o potencial inicial é:
Enquanto o ponto final está sob uma linha de potencial igual a , então sabemos que o potencial final é:
A variação de potencial elétrico é igual a:
Substituindo os valores que já encontramos pela figura:
Resultando em:
E o que fazemos com os potenciais que a carga passou até chegar no final?? Bem... nada hehe Só precisávamos mesmo dos pontos inicial e final.
Passo 3
E como relacionamos a diferença de potencial e o trabalho realizado para levar a carga ? Simples, através da fórmula:
O enunciado já nos deu o valor da carga :
Enquanto já tínhamos o valor da diferença de potencial ,
Como precisamos do na fórmula, vamos multiplicar tudo por :
A multiplicação entre dois números negativos resulta em um número positivo:
Logo, vamos aplicar esses valores na equação:
Passo 4
Para calcular isso, vamos multiplicar primeiro por :
Substituindo, temos:
Não está exatamente da forma como as opções são dadas, não é?
Quando a vírgula não é escrita, secretamente ela está depois do último dígito. Nesse caso, a vírgula estaria depois do do . Precisamos passar ela para depois do , mas temos que fazer isso dentro da legalidade matemática, beleza?
Uma dica para mover a vírgula é a seguinte:
- Quero mover a vírgula casas para a esquerda Tenho que somar no expoente do .
- Quero mover a vírgula casas para a direita Tenho que subtrair no expoente do .
Onde o pode ser qualquer número de casas que você queira andar com a vírgula.
No nosso caso, precisamos andar casa para a esquerda, então temos que somar no expoente do , sacou?
Então o expoente do será
Chegamos na Letra !