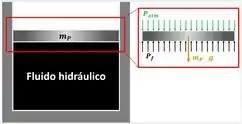
Um conjunto cilindro-pistão vertical apresenta diâmetro igual a e contém fluido hidráulico. A pressão atmosférica é igual a . Determine a massa do pistão sabendo que a pressão no fluido é igual a . Admita que a aceleração da gravidade seja a “normal”.
Passo 1
O problema pede a massa do pistão, que, somada à força atmosférica, produzirá uma pressão de no fluido hidráulico. Para encontrar uma equação que relacione a massa com esa pressão, aplicaremos a segunda lei de Newton no pistão.
onde:
- é a massa do pistão, que é a incógnita do problema
- é a força resultante sobre o pistão
- é a aceleração do pistão
O exercício não fala sobre o movimento do pistão. Por isso, sua aceleração deve ser nula.
Nessa condição:
Além disso, a força resultante é igual à diferença entre a força gerada pela pressão do fluido hidráulico e a soma das forças peso do pistão e atmosférica.
sendo:
- a aceleração da gravidade de
- a força gerada pela pressão do fluido.
- a força gerada pela pressão atmosférica sobre o pistão
O cálculo dessas forças e relação entre elas, ficarão para o próximo passo.
Passo 2
A força causada pela pressão do fluido é dada pela fórmula:
onde:
- é a pressão do fluido sobre o pistão. Essa variável vale ;
- é a área do pistão sobre a qual a pressão do líquido atua.
Essa área é encontrada a partir da seguinte fórmula:
onde é o diâmetro do pistão. Ele mede .
Para achar a massa rearranjamos o balanço de foças mostrado antes.
A única variável que falta pro cálculo da pressão é a força atmosférica.
sendo a pressão atmosférica de .
Substituindo na expressão da massa do pistão:
No próximo passo substituiremos os dados nessa equação.
Passo 3
Temos que começar com o cálculo da área do pistão.
Substituindo os valores na equação desenvolvida para a massa do pistão: