A pressão máxima no fluido utilizado num macaco hidráulico é . Sabendo que o macaco deve levantar um corpo com massa de 850 kg, determine o diâmetro do conjunto cilindro-pistão que movimenta o corpo.
Passo 1
O problema pede o diâmetro do êmbolo necessário para levantar um corpo pesado sem ultrapassar a pressão máxima que o fluido, presente dentro do conjunto cilindro-pistão, suporta.

Ou seja, precisamos descobrir uma área que faça a pressão do fluido vencer a força que o peso do corpo impõe ao pistão.

Para calcular a área precisamos calcular a força provocada pela pressão do fluido. Para calcular essa força, precisamos aplicar a segunda lei de Newon sobre o pistão.
onde é a força resultante sobre o pistão, é a massa do pistão e é a aceleração do êmbolo pra cima.
Como faremos esse cálculo se não temos nenhuma dessas informações? Não sabemos a força resultante, porque não conhecemos o peso do próprio pistão. Não sabemos sua massa, nem sua aceleração.
Resolvemos esse impasse através de uma informação escondida no enunciado: a massa do pistão é desprezível!
Isso pode ser deduzido, porque sem essa simplificação, não seríamos capazes de resolver a questão e, além disso, o peso do que queremos levantar deve ser sempre muito maior do que o peso da ferramenta que usamos para levantar. Caso contrário estaríamos sendo ineficientes.
Passo 2
Com essa informação adicional aplicamos a segunda lei de Newton no êmbolo:
Onde é a força que a pressão do fluido exerce sobre o pistão e é a força de contato entre o corpo erguido e o êmbolo.
A força é encontrada, rearranjando a fórmula de pressão do fluido.
onde é a pressão do fluido e é a área do pistão.
Sua pressão é dada como a máxima pressão que o fluido suporta.
Como o problema pede o diâmetro do pistão, deduzimos que ele é circular. Por isso:
onde é o diâmetro do pistão.
Falta apenas encontrar a para começarmos a substituir todos os valores dados no problema. Fazemos isso aplicando a segunda lei de Newton ao corpo que erguemos.
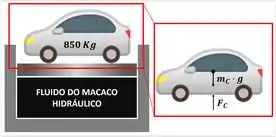
onde é a força resultante sobre o corpo, é a massa do corpo, é a gravidade da Terra, é a massa do corpo e é a aceleração do corpo.
A massa do corpo é dada:
Também sabemos a gravidade da Terra
Só resta a aceleração do corpo para acharmos . Felizmente, seu valor é outra informação escondida no enunciado! Como nós aproximamos os processos termodinâmicos como processos de quase-equilíbrio, consideramos que o corpo está próximo ao equilíbrio. Portanto:
Com essa simplificação:
Passo 3
Enfim podemos substituir os valores para descobrir o diâmetro do pistão. Começamos esse processo a partir do cálculo de .
Lembrando da segunda lei aplicada ao êmbolo, temos:
Com a força da pressão do fluido no cilindro podemos rearranjar o fórmula de pressão para achar a área do pistão.
Reorganizando a fórmula da área e substituindo seu valor, encontramos o diâmetro do pistão.