Um recipiente fechado e com volume de contém de granito e ar (massas específicas respectivamente iguais a e ). Determine a massa de ar contida no recipiente e o volume específico médio do arranjo.
Passo 1
O enunciado pede primeiro que a gente determine a massa de ar do recipiente. Podemos fazer isso, rearranjando a fórmula de massa específica para o ar.
O problema diz o valor de massa específica do ar.
Mas resta saber o valor do volume que o ar ocupa dentro do recipiente . Como o volume total é igual a à soma dos volumes ocupados pelo ar e pelo ar, temos que:
A questão fala pra gente apenas o valor de volume total do recipiente.
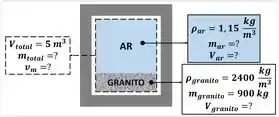
Para saber o volume ocupado pelo granito e descobrir o volume do ar, reorganizamos a fórmula de massa específica do granito.
A massa de granito e sua massa específica foram todas informadas pelo enunciado.
Assim descobrimos o volume de granito. Com esse valor calculamos o valor de volume de ar por fim calculamos a massa de ar.
Passo 2
A segunda etapa do problema é calcular o volume específico médio do conteúdo do recipiente (ar e granito). Fazemos isso através de sua fórmula.
onde é o volume específico médio e é a massa de granito mais a massa de ar.
A massa de ar é calculada no primeiro passo da solução do exercício. O valor de massa do granito é dado pelo problema.
Como o valor do volume total do recipiente também é informado no enunciado, a última etapa é substituir os valores na fórmula de volume específico.
Então vamos substituir os valores dados para descobrir o volume de granito.
Passo 3
Vimos que a primeira etapa para descobrir a massa de ar é saber o volume de granito.
O próxima fase é calcular o volume de ar.
Por fim:
Passo 4
Para chegar ao valor de volume específico médio precisamos primeiro do valor de massa total.
Agora estamos prontos para encontar o volume específico médio.