A figura abaixo mostra um ciclo de potência efetuado por um gás em um conjunto ciclindro-pistão. Para o processo 1-2, . Para o processo 3-1, . Não há variações de energia cinética ou potencial. Determine o trabalho para cada processo, em , e a transferência de calor para os processos 1-2 e 2-3, ambos em .
Passo 1
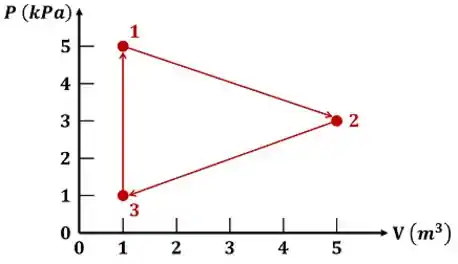
O exercício fala sobre três processos realizados por um gás que completam um ciclo: o gás começa no estado 1, passa pelo processo 1-2 até alcançar o estado 2, percorre o processo 2-3 e, por último, volta para o estado 1 pelo processo 3-1.
Todos os estados são mostrados no gráfico por meio de números ao lados de pontos.
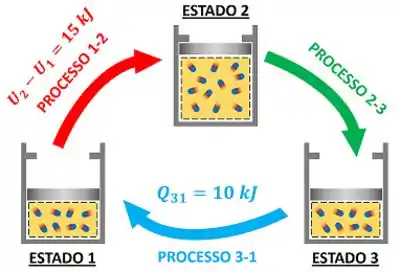
O exercício nos dá informações sobre o calor trocado em alguns processos e sobre a variação de energia interna . Por outro lado, ele pede pra gente calcular o trabalho realizado em todos os processos (, e ) e as trocas de calor restantes ( e ).

Ou seja, a gente precisa de alguma forma ligar as informações dadas com o que a questão pede. A única fórmula que liga trabalho, calor e variação de energia é a primeira lei. Por isso, aplicaremos a primeira lei em todos os três processos.

Para o processo 1-2, a primeira lei tem a seguinte forma:
Para o processo 2-3, ela vira:
Por último, o processo 3-1, a primeira lei é:
onde:
- é a energia cinética do gás;
- é a energia potencial gravitacional do gás.
Para cada processo, nós temos que descobrir a variação de energia cinética causada por ele, a variação de energia potencial gravitacional, a variação de energia interna, o trabalho e o calor trocado.
É muita coisa, não é mesmo? Mas o exercício facilita um pouco o nosso trabalho!

Ele diz que não existe variação das energias cinética e potencial durante os processos. Por causa disso, as fórmulas viram:
Além disso, o enunciado ainda dá diretamente o valor de algumas variáveis.
Pra completar, o problema ainda dá pra gente algumas informações indiretas através do gráfico. Essas informações escondidas fundamentais para calcular o trabalho dos processos. Mas ele não vai ser calculado através de fórmulas. Pra achar , vamos ter que aprender a calcular essa variável graficamente. Isso vai ser feito no próximo passo!
Passo 2
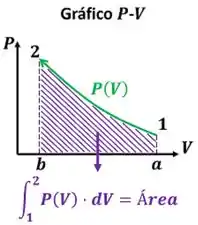
Para calcular graficamente, nós vamos ter que lembrar que o valor absoluto do trabalho é igual à área que está embaixo da curva desenhada pelo processo no gráfico -. A figura abaixo ilustra isso para um processo qualquer.
Agora vamos usar esse conhecimento para calcular .
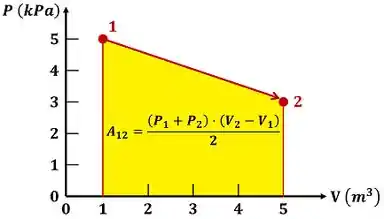
é igual a área do trapézio que está embaixo da reta 1-2 que representa o processo 1-2. Isso acontece, porque no processo 1-2 o volume do gás aumenta. Ou seja, o gás realiza trabalho na vizinhança. Em outras palavras o seu valor é positivo!
Todas as variáveis que estão presentes no cálculo da área são obtidas olhando para o gráfico.
Vamos fazer a mesma coisa com os outros processos!
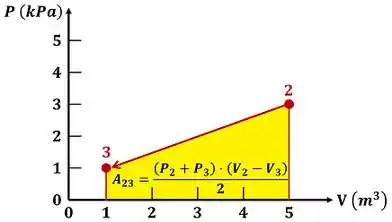
Dessa vez a gente deve tomar cuidado! não é igual a área do trapézio que está embaixo da reta 2-3 que representa o processo 2-3. Isso acontece, porque no processo 2-3 o volume do gás diminui. Ou seja, o gás sofre trabalho da vizinhança. Em outras palavras, o seu valor é negativo!
As variáveis na fórmula dessa área também podem ser encontradas no gráfico.
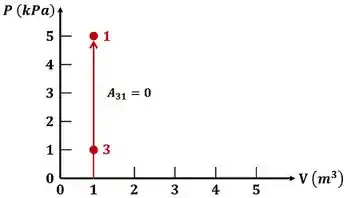
A curva do processo 3-1 não tem área embaixo dela! Por causa disso:
Para finalizar, temos que lembrar que o gás percorre um ciclo! Isso significa que a energia interna final é igual a energia interna final! Em outras palavras, a soma da variação de energia interna de cada processo deve ser nula!
Agora só falta substituir todas esses valores na primeira lei e nas fórmulas do trabalho! Vamos fazer isso no passo seguinte!
Passo 3
Vamos começar pelo cálculo do trabalho de cada processo.
Substituindo na primeira lei, achamos a troca de calor .
Para calcular , temos que calcular antes e .
Usando o valor de na primeira lei do processo 2-3, encontramos: