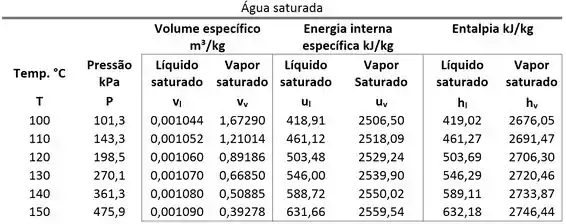
Um vapor d’água saturado contido em um conjunto cilindro-pistão a ocupa de volume. O vapor sofre trabalho e, após esse processo adiabático, ele libera de calor. Considerando que o vapor realiza um ciclo termodinâmico, determine o valor da sua energia interna específica da água logo após ela sofrer trabalho. Utilize a tabela termodinâmica abaixo.
Passo 1
O enunciado diz que o vapor contido no conjunto cilindro-pistão passa por dois processos que formam um ciclo: o processo de sofrer trabalho (processo A) e o processo de liberação de calor (processo B).
Como os dois processos formam um ciclo, o trabalho realizado sobre o sistema durante o processo A é igual ao calor liberado pelo gás durante o processo B . Isso ocorre, porque a primeira lei para um ciclo tem a seguinte forma.
É justamente essa ligação entre os valores de calor e trabalho que nos levará ao valor da energia interna específica do estado 2 .
Sabemos que o vapor perde de energia por calor. Logo, vale:
Já o trabalho só pode ser calculado com a ajuda da primeira lei da termodinâmica aplicada ao processo A.
onde:
- é a troca de calor entre sistema e vizinhança durante o processo A. Como o enunciado diz que esse é um processo adiabático:
- é a massa do vapor em quilograma ;
- é a energia interna específica do vapor antes dele sofre trabalho;
- é a energia interna específica do vapor depois dele sofre trabalho. Ela é a incógnita do problema!
A equação da primeira lei aplicada ao processo A mostra que falta encontrar os valores de e para calcular !
A gente vai aprender a fazer isso no próximo passo.
Passo 2
A massa da água pode ser calculada reorganizando a fórmula e volume específico:
onde:
- é o volume que a água ocupa antes de sofrer trabalho. Segundo enunciado:
- é o volume específico que a água tem antes de sofrer trabalho. Ele é o da tabela de propriedades para de temperatura.
pode ser obtida através da tabela termodinâmica. Ela é a da tabela para .
Se a gente reorganizar a primeira lei para o processo A, conseguimos criar uma fórmula para .
Usando a primeira lei para ciclos, descobrimos que:
Agora podemos substituir os valores que temos nessa fórmula para achar o resultado final.
Passo 3
Iniciamos as contas pelo cálculo da massa . A primeira etapa para isso é achar na tabela de propriedades.
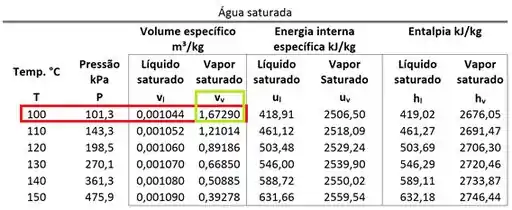
Colocando esse valor na equação de :
está na mesma linha da tabela que o .
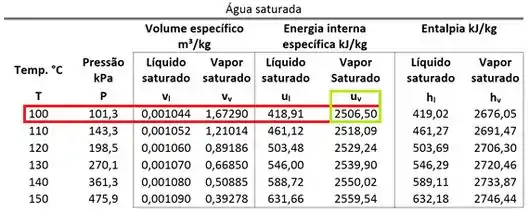
Usando tudo o que temos na fórmula de :
Essa é a resposta que a gente estava buscando!