Um gás contido em um conjunto cilindro-pistão ocupa inicialmente de volume. Ele realiza um processo isobárico a . Ao final desse processo, ele passa a ocupar de volume. Quanto calor ele precisa trocar com o ambiente para completar um ciclo?
Passo 1
O enunciado diz que o sistema realizou um processo a pressão constante de , no qual o volume foi diminuído. Quando o problema diz isso, ele quer dizer que a vizinhança realiza trabalho no sistema! Mas não é qualquer tipo de trabalho! A fronteira do sistema muda de posição, quando o trabalho é realizado. Logo, ele é o trabalho de movimento de fronteira!
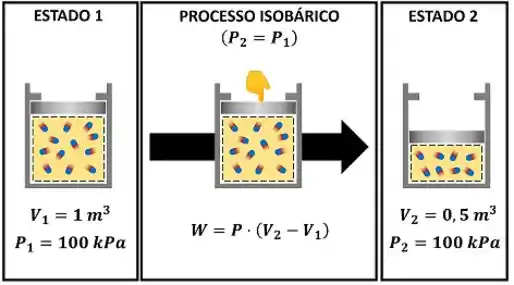
Existe uma fórmula para calcular esse trabalho de movimento de fronteira a pressão constante ! Ela vai ser muito importante na resolução dessa questão!
onde:
- é a pressão do gás durante o processo. Ela vale segundo o enunciado;
- é o volume inicial do gás antes do processo. Ele vale segundo o enunciado;
- é o volume final do gás depois do processo. Ele vale segundo o enunciado.
Mas do que vale saber calcular o trabalho , se nós queremos calcular o calor trocado ?
Responderemos isso no próximo passo!
Passo 2
Essa etapa é importante, porque existe uma fórmula para ciclos que calcula o calor em função do trabalho. Ela se chama primeira lei da termodinâmica e se encontra abaixo!
Substituindo a equação do trabalho de movimento de fronteira na fórmula acima chegamos na seguinte expressão matemática.
Agora é só substituir os dados da questão para achar .
Isso será feito no passo a seguir!
Passo 3
O enunciado diz que:
Antes de substituir esses números na fórmula que criamos, vale fazer uma pergunta: qual será a unidade do calor , se fizermos as contas, usando a unidade da pressão em quilopascal ?
Como a pressão estará em quilopascal a unidade do calor será o quilojoule !
Pronto! Chegamos na resposta final!