Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Princípio da Indução Finita

Ver Teoria
Exercício 912345678

Enunciado

[UFABC] Cálculo 1 - Lista de Exercícios 7

Prove por indução as seguintes propriedades do somatório:

a)

∑ k = 1 n ( a k + b k ) = ∑ k = 1 n a k + ∑ k = 1 n b k

(aditividade)

Passo 1

Fala aí, pessoal inteligente! Vamos fazer uma questãozinha que deixa a galera incomodada por ter que provar, mas vou te mostrar que vai ser moleza!

Bom vamos começar pelo problema inicial que é esse somatório com duas parcelas internas:

∑ k = 1 n a k + b k

Bom, sabemos que o valor de k vai se alterar a partir de 0 até o valor de n , então substituindo esses valores de k no somatório, teremos as parcelinhas:

∑ k = 1 n ( a k + b k ) = a 1 + b 1 + a 2 + b 2 + a 3 + b 3 + … + a n + b n

Passo 2

Você percebe que podemos reorganizar colocando todos as parcelas que tem o fator a em uma soma e as parcelas que dependem de b em outra soma:

∑ k = 1 n ( a k + b k ) = a 1 + a 2 + a 3 + … + a n + b 1 + b 2 + b 3 + … + b n

Olhando com muito carinho temos duas parcelas gigantes, uma em função de a e outra em função de b :

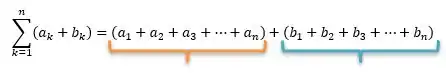
Passo 3

Bom, olhando para essa parcela que marcamos em laranja:

a 1 + a 2 + a 3 + … + a n

Estamos variando o valor do índice de 1 até n nesse somatório, logo, podemos reescrever essa parcela como:

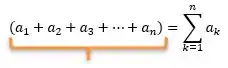
Uhul, podemos repetir isso para a parcela em azul também, pois o padrão se repete:

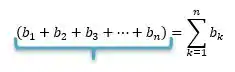
Então vamos voltar para o nosso problema inicial:

∑ k = 1 n ( a k + b k ) = a 1 + a 2 + a 3 + … + a n + b 1 + b 2 + b 3 + … + b n

Substituindo os valores que encontramos:

∑ k = 1 n ( a k + b k ) = ∑ k = 1 n a k + ∑ k = 1 n b k

Chegamos no final do nosso problema e provamos que sabemos muito!

Resposta

Ei, a resposta está no passo a passo :)