Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Princípio da Indução Finita

Ver Teoria
Exercício 612345789

Enunciado

[UFABC] Cálculo 1 - Lista de Exercícios 7

Prove por indução as seguintes propriedades do somatório:

c)

∑ k = 1 n ( a k - a k - 1 ) = a n - a 0

(telescópica)

Passo 1

Fala aí, pessoal! Vamos usar a essa questão para aquecer nossas cabecinhas para receber mais conhecimento!

Começando pelo somatório da questão:

∑ k = 1 n a k - a k - 1

Vamos substituir o valor de k de 1 até n :

∑ k = 1 n a k - a k - 1 = a 1 - a 1 - 1 + a 2 - a 2 - 1 + a 3 - a 3 - 1 + … + a n - 1 - a n - 1 - 1 + ( a n - a n - 1 )

Antes de resolver qualquer coisa, vamos calcular os índices de cada elemento, porque está uma verdadeira bagunça, mas não por muito tempo:

∑ k = 1 n a k - a k - 1 = a 1 - a 0 + a 2 - a 1 + a 3 - a 2 + … + a n - 1 - a n - 2 + ( a n - a n - 1 )

Agora sim, podemos continuar!

Passo 2

Percebe aqui uma coisa comigo, temos parcelas que tem o mesmo valor, porém com sinais diferentes:

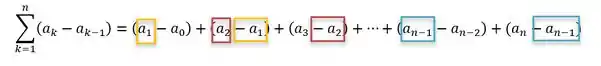
Você concorda comigo, que se temos duas parcelas que se somam, se elas têm valores iguais, porém com sinais diferentes, a soma é igual a zero? Olha aqui:

a 1 + - a 1 = a 1 - a 1 = 0

Veja que o primeiro item da primeira parcela sempre se cancela com o segundo item da próxima parcela:

Logo, se nós olharmos para o nosso somatório, vamos cancelar as parcelas que nós sabemos que serão cortadas:

∑ k = 1 n a k - a k - 1 = a 1 - a 0 + a 2 - a 1 + a 3 - a 2 + … + a n - 1 - a n - 2 + ( a n - a n - 1 )

Passo 3

Ou seja, as parcelas que nos restam são apenas essas duas:

∑ k = 1 n a k - a k - 1 = - a 0 + a n

Reorganizando essas parcelas, chegamos a:

∑ k = 1 n a k - a k - 1 = a n - a 0

Chegamos no final e arrasamos tanto que somos dignos do martelo do Thor! Vai com tudo pra próxima questão, amigão!

Resposta

Ei, a resposta está no passo a passo :)