Um conjunto cilindro-pistão termicamente isolado está inicialmente evacuado e começa a ser preenchido com ar a . Quando o ar contido no conjunto atinge de temperatura, o abastecimento de ar é interrompido. Neste instante, o ar do cilindro-pistão ocupa um volume igual a e possui uma pressão de . Determine o trabalho realizado pelo ar ao empurrar o pistão.
Passo 1
Galera, pra entender o enunciado, vamos resumir tudo! Ar a entra em um conjunto cilindro pistão inicialmente sem ar (massa inicial ) até o conjunto ficar com ar a , e ocupar um volume . Nesse enchimento, o ar realiza um trabalho que precisamos calcular. A figura abaixo ilustra esses dados.
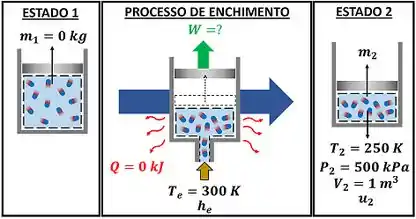
O calor trocado entre o ar e o ambiente vale zero, porque o conjunto cilindro-pistão está isolado termicamente.
Para achar o valor do trabalho realizado pelo ar sobre o pistão, temos que aplicar a lei de conservação de energia no conjunto.
Substituindo e nessa equação, achamos uma fórmula pra .
Ou seja, temos que achar , , e pra calcular ! Acharemos e na próxima etapa!
Passo 2
Achamos e , usando a fórmula de energia interna e entalpia de gases perfeitos com calores específicos constantes. Essas fórmulas são mostradas abaixo.
onde é o calor específico a pressão constante do ar que vale e é o calor específico a volume constante do ar que vale .
Substituindo os valores, encontramos:
Agora só falta achar e pra calcular . Então partiu fazer isso no passo seguinte!
Passo 3
Nós podemos calcular a massa de ar que o cilindro-pistão passa a ter depois de ser abastecido, usando a equação de gases perfeitos no estado 2 do ar.
onde é a constante de gás do ar que vale .
Substituindo os valores na fórmula de , achamos:
A quantidade de massa que o conjunto recebe de ar é igual à massa de ar que o cilindro-pistão passou a ter depois do abastecimento menos a quantidade de ar que o conjunto tinha antes. Logo:
Substituindo os valores na fórmula de :
Shoooooow! Calculamos o trabalho realizado pelo ar! Pode comemorar!