Um recipiente rígido, inicialmente em vácuo, é carregado com água, proveniente de uma tubulação, a e . Admita que o processo de enchimento é adiabático e que o recipiente é lacrado quando a pressão interna for igual à da linha. Sabendo que a massa contida no recipiente após o término da operação de enchimento é igual a , determine a temperatura final do processo de enchimento e o volume do recipiente.
Passo 1
Oi gente! Animad@s pra fazer um exercício de processo em regime transiente?
O exercício quer saber quanto vale a temperatura da água no tanque após ele ser abastecido com água a e . Ele também quer saber quanto vale o volume do tanque. A figura abaixo mostra os dados que temos pra calcular e .
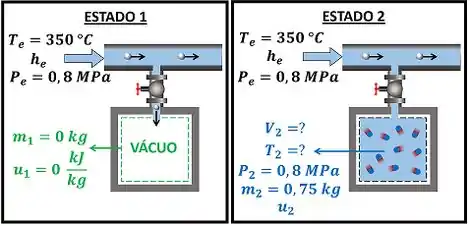
Através da figura, vemos que a água do tanque estava no estado 1 e passa para o estado 2 depois de ser abastecido com água. , e são a temperatura, a pressão e a entalpia da água que entra no tanque. Para achar o valor da temperatura da água após o abastecimento, temos que aplicar a lei de conservação de energia no tanque:
é o calor trocado entre a água e o ambiente. Ele vale zero, porque o processo de enchimento é adiabático. Além disso, como o tanque é rígido, a água do tanque não muda seu volume. Logo, a água não realiza trabalho de movimento de fronteira. Em outras palavras, vale zero. Subsituindo esses dados:
Além disso, como o tanque estava vazio no início do enchimento, a massa de água inicial no tanque vale zero, assim como a energia interna inicial da água no tanque.
Reorganizando essa equação, achamos uma fórmula para a energia interna que a água do tanque tem após o enchimento do tanque.
Com e , podemos usar a tabela de propriedades da água e achar o valor de !
No próximo passo acharemos e para conseguir calcular e encontrar através da tabela!
Passo 2
A quantidade de massa que o tanque recebe de água é igual à massa de água que o tanque passou a ter depois do abastecimento menos a quantidade de água que o tanque tinha antes. Logo:
Substituindo na fórmula de , descobrimos que:
é a entalpia específica do vapor d’água superaquecido a e que entra no tanque. A água está superaquecido, porque sua temperatura é maior que a temperatura de saturação de da água a pressão de .
Logo, achamos na tabela de vapor superaquecido da água a e .
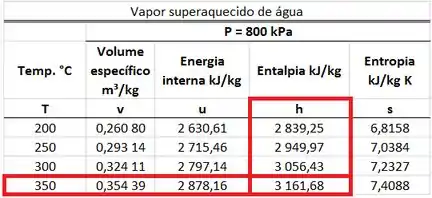
Agora sim podemos achar e no próximo passo.
Passo 3
Como é igual a , temos que vale:
Já sabemos que a pressão da água no tanque após o enchimento vale e que a energia interna da água após o enchimento do tanque vale . Com essas informações, somos capazes de determinar se a água é um vapor superaquecido ou é saturada, comparando com a energia interna do vapor saturado a .
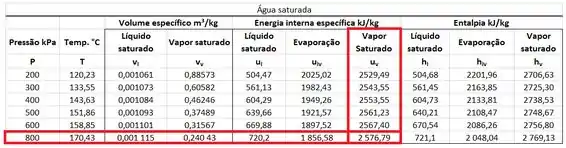
Comparando com , descobrimos que a energia interna é maior. Isso quer dizer que a água do tanque após o enchimento é um vapor superaquecido.
Logo, achamos interpolando a tabela de vapor superaquecido da água que tem e .
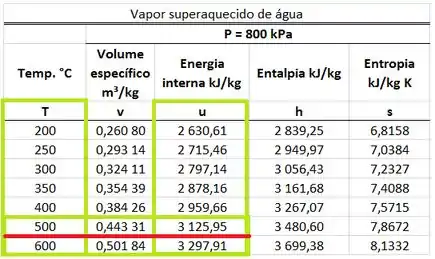
Oba! Achamos a primeira informação que o enunciado nos pediu! Agora, vamos calcular o volume do tanque!
Passo 4
O volume do tanque que a água ocupa após o enchimento pode ser calculado através da fórmula do volume específico do vapor superaquecido d’água.
Achamos o valor de , interpolando a tabela de vapor superaquecido d’água, usando o valor da energia interna que possuímos.
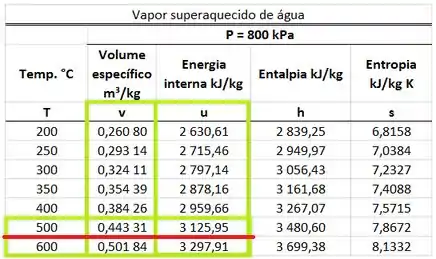
Substituindo na equação de , achamos:
Boaaaaa! Achamos a segunda e última informação que o enunciado nos pediu! Agora é só correr pro abraço!