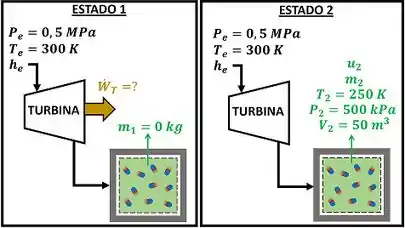
A Fig. P6.119 mostra o esquema de uma turbina que é alimentada com a e . A descarga da turbina está ligada a um tanque com volume de , e que inicialmente está evacuado. A operação da turbina termina quando a pressão no tanque atinge . Nesta condição, a temperatura do no tanque é de . Admitindo que todos os processos são adiabáticos, determine o trabalho realizado pela turbina num processo de enchimento do tanque.
Passo 1
Pessoal, tudo joinha? Vamos resumir esse enunciado e entender o que ele nos deu de dado? Resumindo tudo, o enunciado disse que a e pressão passa pela turbina, gerando um trabalho desconhecido, e enche um tanque inicialmente sem (massa inicial ). O tanque para de encher, quando o alcança o estado 2 abaixo.
O calor trocado entre o e o ambiente vale zero, porque o enunciado diz que todos os processos são adiabáticos.
Para achar o valor do trabalho que foi pedido , temos que aplicar a lei de conservação de energia no conjunto formado pela turbina e pelo tanque.
Substituindo e nessa equação, achamos uma fórmula pra .
Ou seja, temos que achar , , e pra calcular ! Acharemos e na próxima etapa!
Passo 2
Achamos e , usando a fórmula de energia interna e entalpia de gases perfeitos com calores específicos constantes. Essas fórmulas são mostradas abaixo.
onde é o calor específico a pressão constante do que vale e é o calor específico a volume constante do que vale .
Substituindo os valores, encontramos:
Agora só falta achar e pra calcular . Então partiu fazer isso no passo seguinte!
Passo 3
Nós podemos calcular a massa de que o tanque passa a ter depois de ser abastecido, usando a equação de gases perfeitos no estado 2 de .
onde é a constante de gás do que vale .
Substituindo os valores na fórmula de , achamos:
A quantidade de massa que o tanque recebe de é igual à massa de que o tanque passou a ter depois do abastecimento menos a quantidade de que o tanque tinha antes. Logo:
Substituindo os valores na fórmula de :
Aaaaaaaaa, garot@! Conseguimos! Achamos o trabalho realizado pelo !