Um tanque rígido de aço, isolado, com contém ar a . A temperatura do ar é igual a . O tanque está ligado, através de uma ramificação com válvula, a uma linha onde ar escoa a e . A válvula é aberta, permitindo o escoamento de ar para o tanque, e só é fechada quando a pressão interna atinge . Determine a temperatura no instante em que a válvula é fechada.
Passo 1
E aí, galera! Tudo fluindo? Partiu fazer um exercício de processo em regime transiente?
O exercício quer saber quanto vale a temperatura do ar no tanque após ele ser abastecido com ar a e , fazendo o ar ficar com uma pressão de .
A figura abaixo mostra os dados que temos pra calcular .
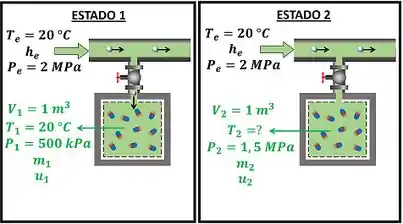
Através da figura, vemos que o ar do tanque estava no estado 1 e passa para o estado 2 depois de ser abastecido com ar. Para achar o valor da temperatura do ar após o abastecimento, temos que aplicar a lei de conservação de energia no tanque:
é o calor trocado entre o ar e o ambiente. Ele vale zero, porque o tanque está isolado. Além disso, como o tanque é rígido, o ar não muda seu volume. Logo, o ar não realiza trabalho de movimento de fronteira. Em outras palavras, vale zero. Subsituindo esses dados:
Até agora temos uma equação em que a temperatura que queremos não aparece. Nós fazemos aparecer, calculando as energias internas e e a entalpia através dos calores específicos, conforme mostrado pelas fórmulas abaixo.
onde é o calor específico a pressão constante do ar que vale e é o calor específico a volume constante do ar que vale .
Com todas essas informações em mãos, podemos começar a tentar a achar no próximo passo.
Passo 2
Para achar a temperatura através da lei de conservação de energia, temos que colocar todas as variáveis dessa equação em função de . Já conseguimos colocar , e em função de . Falta achar , usando as equações de gás perfeito nos estados 1 e 2 do ar.
onde é a constante de gás do ar que vale .
Para usar essa fórmula, precisamos converter de pra somando a .
Aplicando a equação de gases perfeitos no estado 2 do ar:
A quantidade de massa que o tanque recebe de ar é igual à massa de ar que o tanque passou a ter depois do abastecimento menos a quantidade de ar que o tanque tinha antes. Logo:
Agora sim podemos achar através da lei de conservação de energia.
Passo 3
Substituindo os termos em função de na equação de conservação de energia:
Multiplicando os dois lados da equação por :
Para usar essa fórmula, precisamos primeiro converter a pressão de pra , multiplicando por . Depois, convertemos e de pra , somando e a .
![]()
Aeeee! Conseguimos achar e acabar o exercício! :)