Um tanque rígido, com capacidade de , contém ar a e . Uma válvula do tanque é aberta e o ar escoa para fora do tanque até que a pressão atinja . Calor é transferido ao ar, de um reservatório térmico que apresenta temperatura igual a , durante todo o processo. Sabendo que a temperatura final do ar no tanque é , determine a transferência de calor no processo.
Passo 1
Oi, lind@s! Tudo sereno? Vamos direto pro que interessa?
O exercício quer saber quanto vale o calor que o ar do tanque troca com o ambiente durante o processo de esvaziamento do tanque.
A figura abaixo mostra alguns dados que temos pra calcular .
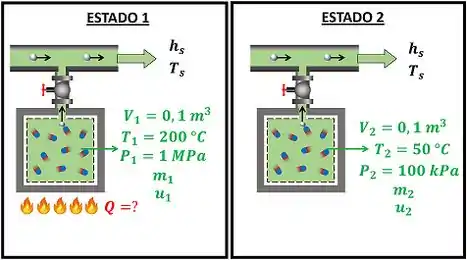
Através da figura, vemos que o ar o tanque estava no estado 1 e passa para o estado 2 depois de ser esvaziado. e são a temperatura e a entalpia do ar que está escapando do tanque rígido. Para achar o valor dado calor trocado , temos que aplicar a lei de conservação de energia no tanque.
Como o tanque é rígido, o ar não muda seu volume. Logo, ele não realiza trabalho de movimento de fronteira. Em outras palavras, vale zero.
Subsituindo esse dado e reorganizando a equação, achamos uma fórmula pra .
Pra achar , temos que achar , , , , e . Vamos começar a fazer as contas, encontrando e no próximo passo.
Passo 2
Para encontrar , temos que interpolar a tabela de gás perfeito do ar.
Antes disso, temos que converter a temperatura de pra , somando a .
Agora nós podemos ver quanto vale na tabela abaixo.
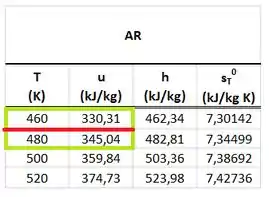
Achamos o valor da massa de ar, usando a equação de gases perfeitos abaixo.
onde é a constante de gás do ar que vale .
Para usar essa equação, temos que converter de pra , multiplicando por .
Pronto, concluímos a primeira etapa pra achar ! No próximo passo vamos achar e !
Passo 3
Para encontrar , temos que interpolar novamente a tabela de gás perfeito do ar.
Antes disso, temos que tomar aquele cuidado de converter a temperatura de pra , somando a .
está na tabela abaixo.
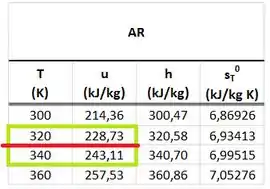
Achamos o valor da massa de ar, usando a equação de gases perfeitos abaixo.
Substituindo os valores que temos:
Depois de achar todos esses valores, resta apenas encontrar e ! Partiu fazer isso no passo seguinte!
Passo 4
A quantidade de massa que o tanque perde de ar é igual à massa de ar que o tanque tinha antes do esvaziamento do tanque menos a massa de passou a ter depois do esvaziamento. Logo:
é a entalpia do ar que sai do tanque durante o esvaziamento. Como a temperatura do ar no tanque varia de a , a entalpia do ar que sai do tanque também varia de a . Logo, usaremos para o cálculo de uma entalpia média entre e .
e são encontrados interpolando a mesma tabela que encontramos e para as temperaturas e .
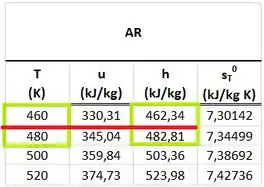
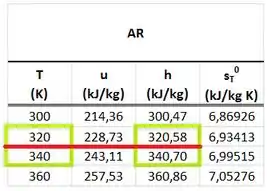
Com esses dados vemos que vale:
Substituindo todos os valores que achamos na fórmula de :
Até que enfiiim! Demorou mas encontramos o que a gente tanto suou pra achar!