Inicialmente, um conjunto cilindro-pistão que opera a pressão constante, contém de água a e . Existe no conjunto cilindro-pistão uma válvula que pode descarregar a água contida no conjunto na atmosfera . Esta válvula é aberta e só é fechada quando a massa contida no conjunto se torna igual a . Admitindo que o processo é adiabático, que a temperatura da água é sempre uniforme, determine a velocidade de descarga da água e o trabalho realizado no processo.
Passo 1
Oier, fofões! Empolgad@s pra fazer um exercício de processo em regime transiente?
A primeira informação que vocês precisam entender é que, quando o enunciado diz que a temperatura da água é uniforme, ele quer dizer que a temperatura da água permanece constante durante todo processo de esvaziamento do cilindro-pistão.

O exercício quer saber primeiro quanto vale o trabalho realizado sobre a água do cilindro durante a saída de água a pressão do conjunto cilindro-pistão. Depois, a questão quer que a gente descubra a velocidade de saída da água.
A figura abaixo mostra os dados que temos pra calcular e .
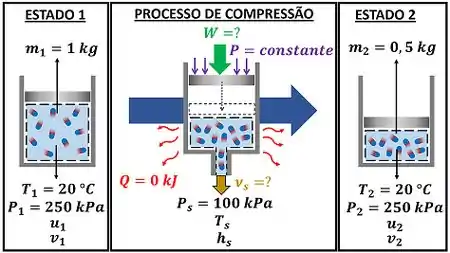
vale zero, porque o enunciado diz que o processo é adiabático.
Para achar o valor do trabalho , vamos usar a fórmula de trabalho de fronteira a pressão constante, porque o enunciado informa que o conjunto cilindro-pistão opera a pressão constante.
onde é o volume que a água ocupa no cilindro depois do esvaziamento e é o volume que a água ocupava no cilindro antes do esvaziamento.
Pra encontrar a velocidade da água saindo do cilindro, temos que aplicar a lei de conservação de energia no conjunto cilindro-pistão.
Ou seja, pra encontrar , temos que achar antes. Por isso, iniciaremos as contas determinando no próximo passo.
Passo 2
Pra encontrar os volumes que a água ocupava e que a água passou a ocupar e determinar , temos que usar as equações dos volume específicos (que a água tinha) e (que a água passou a ter).
Isso quer dizer que pra achar e , precisamos achar e . é o volume específico da água líquida comprimida a e e é o volume específico da água líquida comprimida a e . Se você observar bem, verá que as temperaturas e pressões são iguais. Logo, o estado 1 é igual ao estado 2 da água e temos que:
Ou seja, vamos obter os dois volumes específicos ao mesmo tempo, usando a tabela de propriedades da água. Como não existe uma tabela de água líquida comprimida para uma pressão tão baixa quanto , assumimos que o volume específico da água líquida comprimida, é igual ao volume específico da água líquida saturada a .
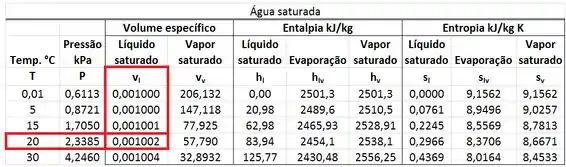
Substituindo essa informação nas equações de e :
Agora podemos achar o valor do trabalho , substituindo e na fórmula de .
Com esse valor em mão, só falta achar , , e pra encontrar . Acharemos esses valores no próximo passo.
Passo 3
A quantidade de massa que o cilindro-pistão perde de água é igual à massa de água que o cilindro pistão tinha antes do esvaziamento menos a quantidade de água que o cilindro-pistão passou a ter. Logo:
As energias internas específicas e são iguais, porque vimos que os estados 1 e 2 são iguais.
Vamos obter e , usando a tabela de propriedades da água. Como não existe uma tabela de água líquida comprimida para uma pressão tão baixa quanto , assumimos que a energia interna específica da água líquida comprimida, é igual à energia interna específica da água líquida saturada a .
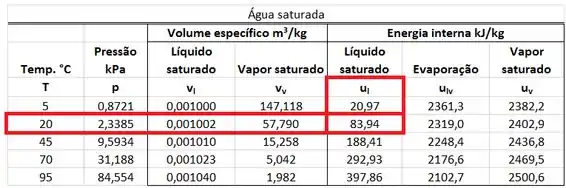
Para encontar a entalpia da água que sai do cilindro, temos que notar que a temperatura da água que sai do cilindro é igua à temperatura da água que está dentro do cilindro.
Isso significa que a água que sai do cilindro é um líquido comprimido a e . Como não existe uma tabela de água líquida comprimida para uma pressão tão baixa quanto , assumimos que a entalpia específica da água líquida comprimida , é igual à entalpia específica da água líquida saturada a .
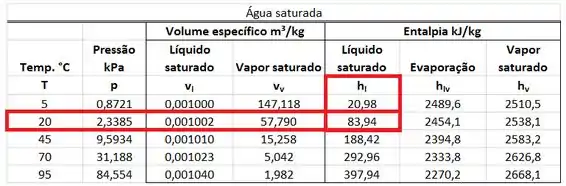
Antes de substituir todos os valores na fórmula de , precisamos converter de pra , multiplicando por e precisamos converter , e de pra , multiplicando esses três termos por .
Uhuuuul! Depois de tanto sufoco conseguimos finalmente achar tudo o que o enunciado pediu pra gente!