Enunciado
Química - Fundamentos de química analítica, Skoog- Ed: 8º - Capítulo 7.Questões e Problemas - Ex. 30
Três métodos analíticos diferentes são comparados em relação à determinação de Ca. Estamos interessados em saber se os métodos diferem entre si. Os resultados, expressos em ppm de Ca, representam determinações por colorimetria, titulação com EDTA e espectrometria
de absorção atômica.
- Defina as hipóteses apropriadas.
- Determine se existem diferenças significativas entre os três métodos a níveis de confiança de 95% e 99%?
- Se foi detectada a diferença a um nível de confiança de 95%, determine quais métodos diferem dos outros.
Passo 1
Oii galerinha, espero que estejam todos bem, e vem comigo resolver este exercício.
Primeiramente iremos relembrar algumas regrinhas. Como podemos perceber no nosso exercício queremos comparar se os métodos diferem entre si, sendo assim, iremos o utilizar A análise de variância (ANOVA) para testar se existe diferença nas médias de mais de duas populações.
No item (a) queremos definir as hipóteses apropriadas, onde a hipótese nula () é quando duas ou mais quantidades observadas são iguais e a hipótese alternativa () é o complemento da hipótese nula, então para nosso exercício temos que:
Passo 2
No item (b) precisamos saber se existe diferença significativa entre os métodos, para isso iremos preencher o quadro abaixo passo a passo:
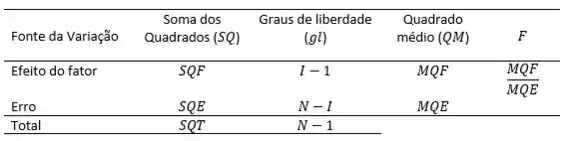
Para fazer esses cálculos iremos precisar do cálculo da média e do desvio padrão de cada método, para isso iremos utilizar as equações:
Então temos o seguinte:
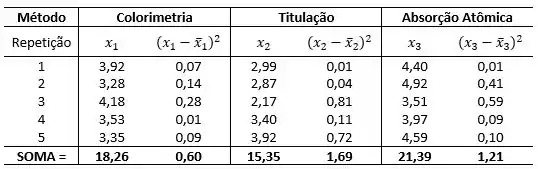
Para colorimetria:
Para titulação com EDTA:
Para absorção atômica:
Agora conseguimos calcular a média global
Passo 3
Com isso iremos calcular a soma dos quadrados do fator ():
O SQF está associado com .
E a soma dos quadrados do erro ():
Que está associado com .
Agora podemos calcular os valores médios quadrados e :
O valor é obtido a partir da seguinte equação:
Completando nossa Tabela ANOVA:
Pela Tabela de distribuição F, para 95% e 99% de confiança com 2 e 12 graus de liberdade, temos:
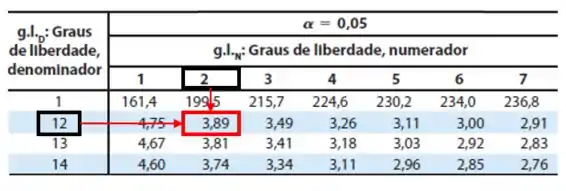
Para um nível de confiança de 95%, o valor crítico de é 3,89. Uma vez que é maior que 3,89, rejeitamos e concluímos que existe diferença significativa entre os métodos.
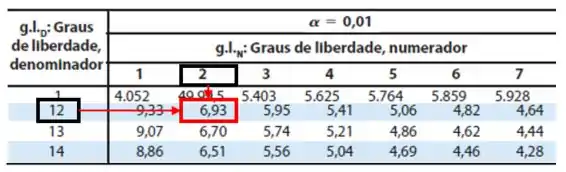
Já para o nível de confiança de 99%, o valor crítico de é 6,93. Como é menor que 6,93, aceitamos e concluímos que não existe diferença significativa entre os métodos.
Passo 4
Como houve diferença a um nível de confiança de 95%, no item (c) precisamos determinar quais são os métodos que diferem. Primeiro iremos organizar as médias em ordem crescente: 3,07; 3,65; 4,28. Como foi realizada 5 repetições para cada método, podemos utilizar a equação da diferença menos significativa ():
Onde:
número igual de réplicas em cada grupo;
quadrado da média para o erro
com graus de liberdade relativo ao erro.
Pela Tabela da distribuição com 12 graus de liberdade e 95% de confiança:
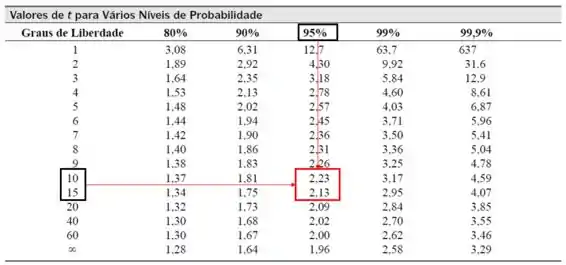
Podemos observar que não há valor para 12 graus de liberdade, então precisamos interpolar esses valores, fiquem tranquilos que irei ajudar:
Logo:
Agora calculamos as diferenças nas médias e comparamos com 0,75. Para vários pares:
;
;
.
(diferença significativa)
(diferença não significativa)
(diferença não significativa)
A partir dos resultados concluímos que o 3° método (absorção atômica) diferencia do 2° método (titulação com EDTA). Porém o 2° e o 3° não se diferenciam do 1° método (colorimetria).
Ufa, finalmente acabamos! Eu sei que esse foi complicadinho, mas espero ter conseguido te ajudar. Até mais pessoal.
Resposta
- ;
- Há diferença significativa para o nível de confiança de 95%, porém para 99% notamos que não houve diferença significativa.
- Para um nível de confiança de 95%, o método de absorção atômica diferencia do método de titulação com EDTA.
.