Na temperatura de , encontra-se parcialmente dissociado, onde para a reação . Um recipiente de contém uma mistura em equilíbrio onde a massa de é igual a de . Pede-se:
a) Determine a massa de nesta mistura.
b) Determine as massas em equilíbrio se a este mesmo recipiente, inicialmente vazio, nesta mesma temperatura, fosse adicionado 10,50 g de .
Passo 1
O enunciado tá meio enrolado né? Vamos decifrar um pouquinho. A reação é a seguinte:
E a constante de equilíbrio:
Repara que a unidade de já indica que a nossa fórmula pra ela está correta!
Além disso, temos:
Vamos precisar também da massa molar do iodo. Pela tabela periódica:
Com essas informações já mais claras, podemos determinar o que o enunciado pede! Bora lá.
Passo 2
a) Através da massa de no sistema e de sua massa molar, vamos calcular o número de mols e a concentração desse cara no meio.
Passo 3
Com a concentração de no meio e o valor de , podemos calcular a concentração de , por:
E, com a concentração, descobrimos o número de mols. Em seguida, podemos calcular a massa de presente.
Chegamos na resposta da letra a:
Passo 4
b) E se a massa de fosse g ao invés de ?
Nesse caso, nós teríamos, inicialmente:
Passo 5
Com a concentração de inicial, podemos montar a tabela do equilíbrio:
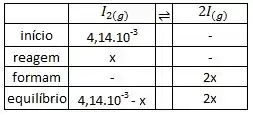
E, com o valor de , calculamos o valor de .
Como o nos leva a valores de concentração negativos, vamos usar o para calcular as concentrações em equilíbrio.
Passo 6
Como se a gente não tivesse feito contas o suficiente, a gente ainda precisa passar esse resultado pra massa de e de no equilíbrio.
A massa de pode ser calculada da mesma forma ou por diferença.
Por diferença:
Resposta
a)
b) e