Avaliar a RGA, e sugerir um esquema de emparelhamento para o seguinte processo:
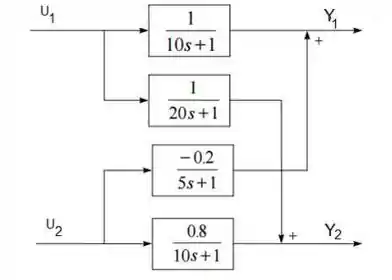
Passo 1
Precisamos calcular a RGA e dizer o melhor emparelhamento para esse conjunto de saídas e entradas. Entretanto, nesse exercício o que foi dado foi como as saídas se relacionam com as entradas sob a forma de diagrama de blocos.
Sendo assim, podemos inferir desse diagrama de blocos que a função de transferência que relaciona a saída com a entrada é:
Da mesma forma a a função de transferência que relaciona a saída com a entrada é:
E analogamente teremos:
Com as funções em malha aberta definidas, é possível determinar a matriz de ganhos em malha aberta.
O ganho em malha aberta é a constante que multiplica a função de transferência, sendo assim podemos gerar uma matriz apenas com os ganhos em malha aberta do processo:
Passo 2
Com todos os ganhos em malha aberta é possível calcular o ganho relativo, através da fórmula abaixo:
Substituindo os calores da matriz de ganho em malha aberta, teremos:
A RGA pode ser calculada então da seguinte forma:
Sendo:
Portanto:
Passo 3
Agora devemos definir qual melhor interação. Para isso devemos seguir duas regras:
- A melhor interação é aquela que tem ganho relativo mais próximo de .
- Evitar ao máximo relacionar variáveis com ganho relativo negativo.
Nesse caso não temos ganho relativo negativo, o qur já facilita o nosso lado. Temos que ver então qual par vai ter ganho relativo mais próximo de .
Sendo assim, o emparelhamento perfeito vai ser entre o 1-1/2-2 uma vez que o ganho relativo para esse emparelhamento será que é mais próximo de do que .
Ou seja, vamos emparelhar a saída com e a saída com .
Resposta
Emparelhamento 1-1/2-2