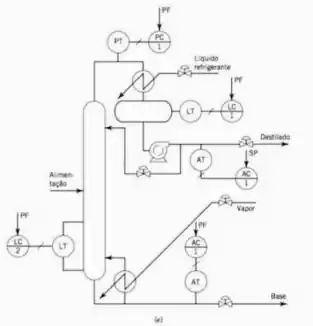
Na coluna de destilação da figura abaixo os fluxos de refluxo e de vapor para o refervedor são manipulados para controlar as purezas do produto destilado e da base. Testes em degrau de malha aberta em cada uma dessas variáveis manipuladas resultam nas seguintes funções de transferência:
One é a composição da porção pesada no destilado, é a composição da porção leve na base, em , e e são os sinais para as válvulas de refluxo e de vapor em . Os parâmetros de tempo estão em horas.
- Calcule os ganhos relativos para este sistema e determine o modo correto de emparelhar as variáveis controladas e manipuladas. As malhas se ajudam ou lutam entre si?
- Faça o diagrama de blocos e o projeto dos desacopladores para este sistema.
Passo 1
Esse exercício tem um monte de informação o que acaba confundindo a gente um pouco. Mas a gente pode dar uma filtrada no que realmente importa.
O fluxograma é bacana para entender melhor o que tá acontecendo e tal mas ele não é super importante para a resolução do exercício.
O que realmente vai importar para nós são as funções de transferência que relacionam cada uma das saídas com as entradas.
Mas porque essas equações são importantes?
Porque a partir dessas equações nós conseguimos encontrar os ganhos em malha aberta e com os ganhos em malha aberta a gente determina quase tudo que o exercício pede da gente.
Os ganhos em malha aberta são as constantes que multiplicam as funções de transferência, sendo assim, a gente consegue montar nossa matriz de ganhos em malha aberta:
Passo 2
Com a matriz de ganhos em malha aberta, conseguimos calcular os ganhos relativos do sistema, que é a primeira coisa que o exercício pede da gente.
Como se trata de um sistema podemos usar a fórmula abaixo para calcular o ganho :
Sunstituindo os valores encontrados anteriormente, teremos:
A matriz de ganhos relativos, também conhecida como RGA, poderá ser definida completamente conforme abaixo:
Sendo .
Portanto:
Boa, já conseguimos a primeira coisa que foi pedido. A segunda é se as malhas se ajudam ou lutam entre sim, que é o mesmo que perguntar se a interação é positiva ou negativa.
Como os ganhos relativos são maiores que ou negativos, dizemos que a interação é negativa, ou seja, elas lutam entre si.
Passo 3
Agora precisamos projetar os desacopladores. Para isso primeiramente vamos ver qual o tipo de interação entre as malhas.
Olhando a matriz de ganhos relativos, podemos ver que o melhor emparelhamento é o do tipo 1-1/2-2. Sendo assim, os desacopladores terão a seguinte fórmula:
Nós podemos pegar essas funções de transferência nas equações que foram dadas pra nós no enunciado, então teremos:
Sendo assim teremos os descopladores:
O decoplador possui um atraso negativo, e isso é fisicamente irrealizável, sendo assim, nós vamos deicar ele apenas como a constante:
Já o desacoplador possui um avanço, que é o termo . Isso não é muito problemático, mas para melhorar o desempenho é legal adicionar nem que seja um atrasozinho. Sendo assim, vamos colocar um atraso pequeno de e acrescentar esse valor no avanço também:
Passo 4
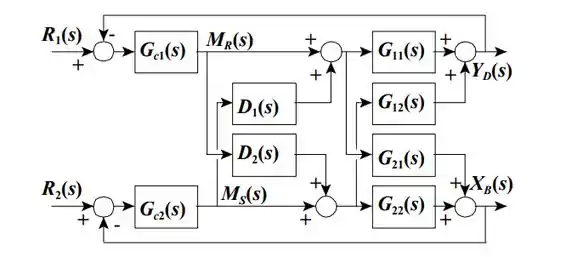
Por último, vamos ver como fica o diagrama de blocos do processo.
D_2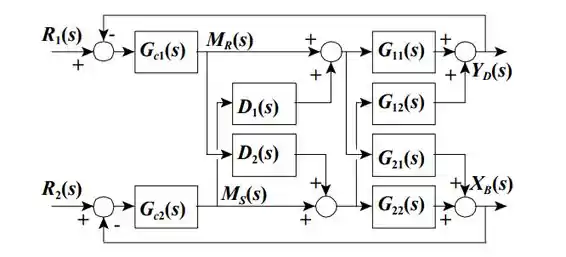
Repare que as malhas estão emparelhadas de forma 1-1/2-2, ou seja, a saída controla e a saída controla .
A entrada ainda assim impacta a sápida através do bloco mas essa interferência é atenuada pelo descoplador , que é o que nós calculamos lá em cima. O mesmo acontece para a entrada .
Resposta
Emparelhamento 1-1/2-2
Interação negativa