Exercícios Resolvidos de Reta Normal e Plano Tangente

Enunciado

2) Seja uma superfície parametrizada por e

Identifique essa superfície

Encontre uma equação da reta normal a em

Encontre uma equação do plano tangente a em

Passo 1

Letra (a)

Essa parametrização olhando rápido parece bem bizarra, né? Mistura funções seno, cosseno e uma parábola ali. Mas vamos lá, vamos tentar entende-la.

Quando fazemos superfície de revolução em torno de algum eixo, é praticamente isso que fazemos! Um termo fica multiplicado por , outro por e outro por nada. No nosso enunciado, a rotação que existe é em torno do eixo z:

Portanto, a curva que deu origem a essa superfície foi:

Uma parábola no plano ! Com isso, a superfície gerada pela sua rotação no eixo é um paraboloide circular. Esse aqui mais precisamente:

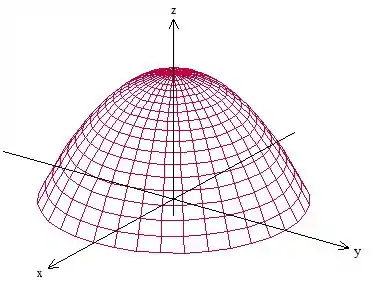
Sua equação é

Passo 2

Letra (b)

Para calcular a equação da reta normal à uma superfície, sabemos que precisamos do ponto que o exercício pede e o vetor normal nesse ponto. Vamos calcular cada um deles e depois descobrir a equação da reta.

Primeiramente, o ponto não foi dado diretamente, mas o enunciado pediu para encontrarmos a reta em , certo? Precisamos então substituir e na parametrização dada, assim olha:

Passo 3

Vamos ao cálculo do vetor normal agora. Sabemos que ele pode ser calculado pela seguinte fórmula

Precisamos calcular essas duas derivadas para depois fazer o produto vetorial:

Esse é o vetor normal para qualquer ponto na superfície, estamos interessados somente no ponto , vamos substituir esses valores ali então:

Passo 4

Tendo o valor da normal e do ponto podemos descobrir a equação da reta normal! Vai ser assim:

Passo 5

Letra (c)

A equação do plano tangente também sabemos fazer, certo? Precisamos também do ponto e do vetor normal no ponto. A fórmula da equação do plano tangente é obtida pelo seguinte produto escalar: