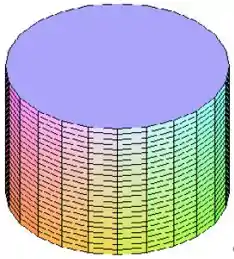
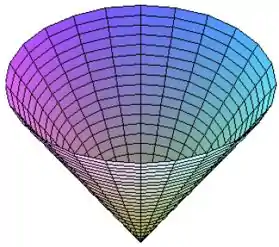
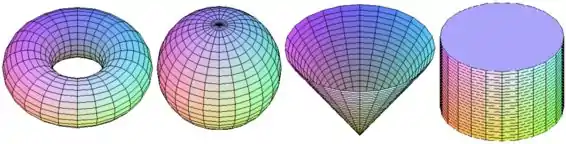
Quais superfícies dadas na figura abaixo correspondem às parametrizações II e IV:
Passo 1
Vamos olhar as parametrizações de e , primeiro com
Repara que temos
Então
Isso é uma circunferência, e ela independe do valor de , ou seja, ela vai ficar sendo repetida para cada valor de entre e , e a figura que fica assim é o cilindro, ou seja, a quarta figura.
Passo 2
Vamos olhar agora a parametrização de
Aqui se temos um seno e cosseno de novo, fazemos e vamos ter
Dessa vez sobrou aquele , mas isso é na nossa parametrização, então vamos ter
E essa equação é de um cone, e dentro das figuras o cone é a terceira figura.
Resposta