A ilustração a seguir representa uma mesa de sinuca retangular, de largura e comprimento iguais a 1,5 e 2,0 m, respectivamente. Um jogador deve lançar a bola branca do ponto e acertar a preta no ponto , sem acertar em nenhuma outra, antes. Como a amarela está no ponto A, esse jogador lançará a bola branca até o ponto , de modo que a mesma possa rebater e colidir com a preta.
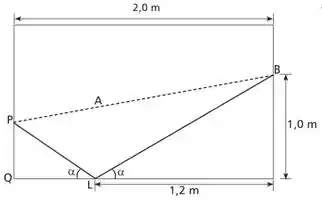
Se o ângulo da trajetória de incidência da bola na lateral da mesa e o ângulo de rebatimento são iguais, como mostra a figura, então a distância de a , em , é aproximadamente:
a) 67
b) 70
c) 74
d) 81
Passo 1
Para encontrarmos o valor da distância, precisamos encontrar dois triângulos semelhantes.
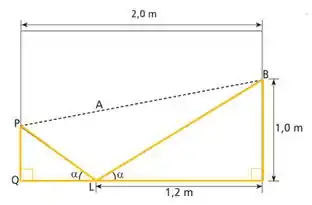
Como na figura os dois triângulos possuem um ângulo de e os dois também possuem um ângulo . Eles seguramente são semelhantes pelo caso AA (Ângulo, ângulo).
Passo 2
Precisamos agora descobrir o valor da distância entre e .
Como sabemos que o comprimento total desse lado da mesa vale metros, o valor da distância de a será:
Passo 3
Finalmente, podemos aplicar uma regra de 3 para descobrir o valor da distância de a :
Multiplicando cruzado, temos:
Resposta
Alternativa a).