Calcule o fluxo do campo
Através da superfície definida pelas equações
Passo 1
Primeiro vamos fazer um rascunho da imagem para entender melhor o problema!
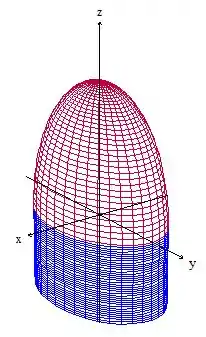
Passo 2
Está vendo a raiz no campo, bom devemos ficar atentos! Raiz e frações são sinais de singularidades, e aqui temos os dois!
O denominador , deve ser diferente de zero! Então o ponto é uma singularidade.
Como dentro da raiz temos uma soma de quadrados, que é sempre maior que zero, a origem é a única singularidade!
Para retirar esta singularidade vamos definir uma esfera centrada na origem de raio bem pequeno!
Assim, o Teorema de Gauss pode ser aplicado como,
Passo 3
Vamos começar calculando o divergente do campo,
Assim,
Passo 4
Agora precisamos calcular o volume do sólido:
Volume do elipsoide, lembra que o volume de um elipsoide é dado por isso aqui?
Onde são as raízes dos denominadores de , e (os semeixos do elipsoide):
Portanto, como queremos metade do elipsoide:
Volume do cilindro elíptico, a área de uma elipse é dada por:
Onde são as raízes dos denominadores de e (os semeixos da elipse), assim, o volume do cilindro é , com , e
Volume da esfera de raio :
Por fim,
Passo 5
Vamos calcular, , que representa o fluxo do campo que passa pela esfera de raio . Para isso vamos parametrizar a esfera por:
Vamos ver quanto dá esse vetor normal da esfera:
Calculando o produto vetorial:
Para resolver esta integral vamos usar:
Ainda,
Assim, teremos:
Como a normal a esta espera está apontando para fora do sólido, o que significa estar apontando para a origem:
Passo 6
Finalmente!! Teremos:
Resposta
Ei, a resposta está no passo a passo :)