Calcule onde e é parte da superfície entre e , orientada de modo que .
Passo 1
Bom, antes de tudo, vamos analisar a superfície que nós temos:
Bom, se a gente não tivese esse termo , isso seria um cone centrado na origem, certo? Então, nossa superfície é um cone deslocado em , centrado em .
Como o enunciado diz, o cone é cortado pelos planos e . Temos então algo assim:
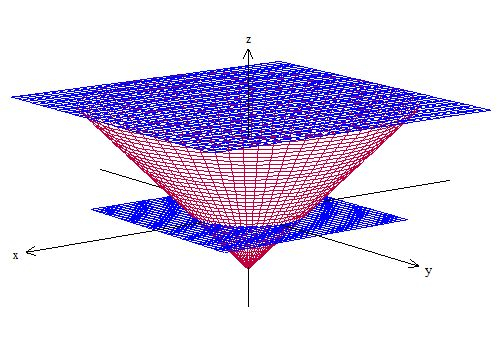
A superfície do problema é a parte do cone que está entre os planos, portanto, um tronco de cone.
Passo 2
Bom, para calcular essa integral de superfície, o primeiro passo é parametrizar esse cone. Como temos no denominador, pensamos logo em coordenadas esféricas, o que faz essa expressão virar apenas . Porém, temos um problema...
Como o cone está deslocado, ele não vai ficar “bonitinho” escrito coordenadas esféricas, como estamos acostumados, vai ficar com uma expressão chata de trabalhar e pior ainda de integrar.
Claro, a gente podia usar as coordenadas esféricas deslocadas para o centro do cone, mas aí, levamos o problema para a expressão do campo! Porque não vai ficar uma expressão nem um pouco amigável se usarmos coordenadas esféricas deslocadas. Ferrou,né?
Bem... talvez tenha uma mateira mais simples de resolver esse problema, vamos calcular o divergente desse campo para ver no que dá:
Podemos escrever o campo como
(Nesse momento que você reza para encontrar uma expressão bonita!)Temos:
Passo 3
Opa! Isso facilita muito nossa vida, não é?? Porque aplicando Gauss, temos:
Ou seja, a integral de superfície desse campo no limite de um volume é igual à integral tripla do divergente de nesse volume.
O que quer dizer que essa superfície deve ser fechada. Beleza, só fechar a nossa superfície, certo? Vamos fechar com esses dois planos que o problema nos deu, os planos e , formando o tronco de cone da figura. Certo?
Muita calma dessa hora, olha a expressão do campo:
Viu que o ponto não está definido? Substituindo ele no campo, temo zero no demoninador.
Bom, então quer dizer que temos que tirar a origem da jogada, ou seja, fechar a nossa superfície deixando a origem fora da região . Bom, vamos envolver a origem com uma esfera então, pode ser? Uma semi esfera, na verdade. Desse jeito aqui:
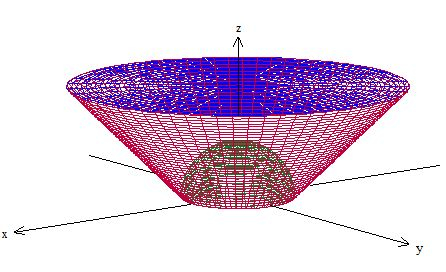
Ou seja, em cima nós fechamos a região com o plano e embaixo com a semiesfera. Aplicando Gauss, temos, então
Sendo a região na figura acima, orientada positivamente. Como queremos a integral na superfície vermelha apenas, temos:
Para termos uma orientação positiva, a normal deve apontar para fora da região. No plano, isso significa apontar para cima, já na esfera e no cone, apontar para baixo.
Mas o problema diz que esse cone tem uma orientação tal que , ou seja, sua normal aponta para cima (para dentro da região). Portanto, queremos:
Onde todo muno está com orientação positiva. Foi?
Passo 4
Bom, então temos que calcular essas duas integrais para conseguir o que queremos. Começando pelo plano.
Temos um círculo planar em . Para descobrir o raio desse círculo, temos que substituir esse valor de na expressão do cone:
Temos, então, um círculo planar de raio em . Parametrizando em coordenadas polares:
Como temos uma volta completa em torno do eixo , . Como já vimos, o raio vai desde a origem até , logo, .
Show? Beleza, agora vamos calcular a normal dessa superfície:
Temos:
Bom, para termos uma orientação positiva da nossa região (como pede o Teorema de Gauss), a normal deve apontar para fora dela, portanto, no plano, deve apontar para cima. Como a coordenada saiu positiva, esse é o vetor certo.
Agora vamos substituir o que encontramos na fórmula:
Onde os intervalos de e são os que encontramos na parametrização.
Escrevendo o campo
Em função das variáveis da parametrização
Temos
Levando para a integral
Fazendo
Passo 5
Agora precisamos resolver a outra integral de superfície, sobre a esfera. Para descobrirmos o raio da esfera, temos que saber o raio do cone quando :
Como o cone acaba em uma circunferência de raio . Vamos fechá-lo com uma esfera do mesmo raio.
Vamos usar coordenadas esféricas para a parametrização:
Com e , já que só temos a parte de cima da esfera.
Como queremos a orientação do vetor para baixo, encontramos o vetor certo.
Para aplicar a fórmula
Temos que escrever o campo em função das variáveis da parametrização:
Como
Isso nos dá
Passo 6
Agora vamos finalmente encontrar o que a gente quer:
Substituindo o que encontramos