Considere o campo Analise as seguintes afirmações:
(I) Se é o elipsoide , com orientado pela normal exterior então
(II) Se é a esfera orientada pela normal unitária exterior então
(III) Se é o cubo de vértices orientado pela normal unitária exterior , então
Podemos afirmar que:
a) apenas a afirmação (I) é verdadeira.
b) apenas as afirmações (II) e (III) são verdadeiras.
c) apenas a afirmação (III) é verdadeira.
d) apenas a afirmação (II) é verdadeira.
e) apenas as afirmações (I) e (II) são verdadeiras.
Passo 1
Cara, ele deu um campo bem estranho né? E pede informações sobre integrais de superfícies em superfícies fechadas com vetor normal exterior. Isso lembra qual Teorema? O Teorema de Gauss! Onde a gente usa esses tipos de superfícies.
Para ver se é interessante usar Gauss aqui, vamos calcular o divergente desse campo. Segura na minha mão:
Ele tem essa fórmulinha:
Então a gente calcula:
Cara, isso vai dar uma conta bem feia, né? Então vou te dar aquele bizu. Guarda no coração: esse campo é feio, mas ele já é conhecido. Ele é o campo elétrico gerado por uma carga em . Os livros de cálculo já falam sobre ele.
E sabe o que eles dizem? Que esse bonito tem divergente igual a zero! Demais né! Se não acredita em mim, repara:
Com esse divergente tranquilinho, certamente vamos usar Gauss então. Bora!
Passo 2
(I) Ele diz que se é o elipsoide , com então
Gauss diz que:
Sendo a região dentro de uma superfície fechada .
Mas a temos um problema. O nosso campo não está definido em (o denominador das componentes zera), então, o elipsoide sozinho não vai ser a fronteira de uma região fechada bem definida em .
Precisamos colocar uma outra superfície fechada dentro dela, que englobe esse ponto. Aí a nossa região vai ser o volume entre essas duas superfícies. Aí vamos considerar que colocar uma esfera de raio dentro desse elipsoide:
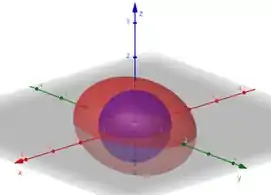
Agora temos duas superfícies como fronteira da nossa região. A esfera (com vetor normal para dentro dela) e o elipsoide. Aí a gente pode montar Gauss assim:
Temos aquele menos ali na esfera porque o seu vetor deve estar apontando para dentro, mas vamos calcular como apontando para fora, aí só mudamos o sinal da integral. E lembrando que :
Passo 3
Então a gente só precisa calcular essa integral dupla da direita. Se a gente parametrizar nossa esfera assim:
O vetor normal e exterior a ela, quando a gente calcula as derivadas parciais, faz o produto vetorial e testa para ver se é o vetor normal exterior mesmo, vai ser
E substituindo a parametrização da esfera no nosso campo:
A gente vê que esse termo dá , porque a equação da esfera de raio 1 diz exatamente isso. Ela diz que . Então essa substituição fica mais tranquila e a gente acha:
Aí montando a integral de superfície:
Passo 4
E calculando:
Daí a gente tira que sendo o elipsoide:
Ou seja, esse primeiro item está errado. Ali, se , dá e não .
Passo 5
(II) Aqui a gente tem essa informação para analisar:
Se é a esfera orientada pela normal unitária exterior então
Cara, repara que essa esfera engloba uma região que não tem o dentro. Olha só ela:
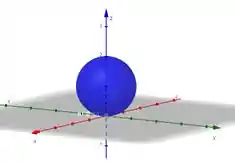
Esse ponto só faz parte da fronteira da esfera. E ele não vai bugar o teorema de Gauss, porque é só um pontinho na superfície e não no meio da região interna.
Aí a para esse cara, a gente pode escrever o teorema de Gauss diretão:
Sendo que é a nossa esfera que limita a região que não tem singularidades no seu interior. E como :
Como o item diz. Então essa é verdadeira.
Passo 6
(III) Essa daí diz que:
Se é o cubo de vértices orientado pela normal unitária exterior , então
Cara, aqui temos o mesmo problema do item (I), a região dentro do cubo não está completamente definida em . Aquele está atrapalhando de novo.
Mas a gente já viu o que fazer com ele né? Vamos colocar uma esfera de raio 1 dentro do cubo, e aí a nossa região vai estar do lado de dentro do cubo e do lado de fora da esfera, e essas duas superfícies serão nossas fronteiras.
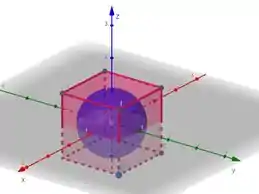
Aí fica assim.
Temos aquele menos ali na esfera porque o seu vetor deve estar apontando para dentro, mas vamos calcular como apontando para fora, aí só mudamos o sinal da integral. E lembrando que :
Mas a gente já achou quando vale essa integral de superfície sobre a esfera! Então:
E aí essa é verdadeira também.
Resposta
Letra b